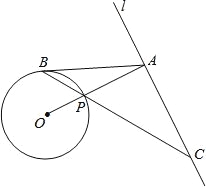
【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长,交直线l于点C,使得AB=AC.
(1)求证:AB是⊙O的切线;
(2)若PC=![]() ,OA=3,求⊙O的半径和线段PB的长.
,OA=3,求⊙O的半径和线段PB的长.
参考答案:
【答案】(1)证明详见解析;(2)![]() .
.
【解析】
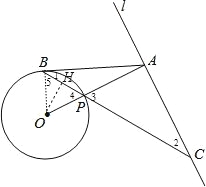
试题分析:(1)连结OB,如图,由等腰三角形的性质得∠1=∠2,∠4=∠5,由OA⊥AC得∠2+∠3=90°,加上∠3=∠4,易得∠5+∠1=90°,即∠OBA=90°,于是根据切线的判定定理可得AB是⊙O的切线;
(2)作OH⊥PB于H,如图,根据垂径定理得到BH=PH,设⊙O的半径为r,则PA=OA﹣OP=3﹣r,根据勾股定理得到![]() ,
,![]() ,所以
,所以![]() ,解得r=1,则PA=2,然后证明Rt△APC∽Rt△HPO,利用相似比可计算出PH=
,解得r=1,则PA=2,然后证明Rt△APC∽Rt△HPO,利用相似比可计算出PH=![]() ,于是得到PB=2PH=
,于是得到PB=2PH=![]() .
.
试题解析:(1)连结OB,如图,
∵AB=AC,
∴∠1=∠2,
∵OA⊥AC,
∴∠2+∠3=90°,
∵OB=OP,
∴∠4=∠5,
而∠3=∠4,
∴∠5+∠2=90°,
∴∠5+∠1=90°,即∠OBA=90°,
∴OB⊥AB,
∴AB是⊙O的切线;
(2)作OH⊥PB于H,如图,则BH=PH,
设⊙O的半径为r,则PA=OA﹣OP=3﹣r,
在Rt△PAC中,![]() ,
,
在Rt△OAB中,![]() ,
,
而AB=AC,
∴![]() ,解得r=1,
,解得r=1,
即⊙O的半径为1;
∴PA=2,
∵∠3=∠4,
∴Rt△APC∽Rt△HPO,
∴![]() ,即
,即![]() ,
,
∴PH=![]() ,
,
∴PB=2PH=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一列式子,按一定规律排列成﹣3a2 , 9a5 , ﹣27a10 , 81a17 , ﹣243a26 , ….
(1)当a=1时,其中三个相邻数的和是63,则位于这三个数中间的数是
(2)上列式子中第n个式子为(n为正整数). -
科目: 来源: 题型:
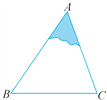
查看答案和解析>>【题目】如图,一块三角形模具的阴影部分已破损.
(1)只要从残留的模具片中度量出哪些边、角,就可以不带残留的模具片到店铺加工一块与原来的模具ABC的形状和大小完全相同的模具A′B′C′?请简要说明理由.
(2)作出模具△A′B′C′的图形(要求:尺规作图,保留作图痕迹,不写作法和证明).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>b,下列关系式中一定正确的是( )
A.a2<b2
B.2a<2b
C.a+2<b+2
D.﹣a<﹣b -
科目: 来源: 题型:
查看答案和解析>>【题目】平方等于16的数是___________,立方等于27的数是___________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学规定学生的学期体育总评成绩满分为100分,其中平均成绩占20%,期中考试成绩占30%,期末考试成绩占50%,小彤的三项成绩(百分制)依次为95,90,88,则小彤这学期的体育总评成绩为 .
-
科目: 来源: 题型:
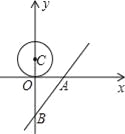
查看答案和解析>>【题目】在平面直角坐标系中,点C的坐标为(0,1.5),我们把以点C为圆心,半径为1.5的圆称为点C的朋友圈,圆周上的每一个点叫做点C的一个好友.
(1)写出点C的两个好友坐标;
(2)直线l的解析式是y=
 x﹣4,与x轴、y轴分别交于A、B两点,圆心C从点(0,1.5)开始以每秒0.5个单位的速度沿着y轴向下运动,当点C的朋友圈有好友落在直线上时,直线将受其影响,求在点C向下运动的过程中,直线受其影响的时间;
x﹣4,与x轴、y轴分别交于A、B两点,圆心C从点(0,1.5)开始以每秒0.5个单位的速度沿着y轴向下运动,当点C的朋友圈有好友落在直线上时,直线将受其影响,求在点C向下运动的过程中,直线受其影响的时间;(3)抛物线y=ax2+bx+c过原点O和点A,且顶点D恰好为点C的好友,连接OD.E为⊙C上一点,当△DOE面积最大时,求点E的坐标,此时△DOE的面积是多少?
相关试题

