【题目】在创建文明城区的活动中,有两端长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度![]() (米)与施工时间
(米)与施工时间![]() (时)之间的关系的部分图像.请解答下列问题.
(时)之间的关系的部分图像.请解答下列问题.
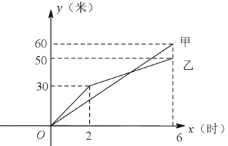
(1)甲队在![]() 的时段内的速度是 米/时.乙队在
的时段内的速度是 米/时.乙队在![]() 的时段内的速度是 米/时. 6小时甲队铺设彩色道砖的长度是 米,乙队铺设彩色道砖的长度是 米.
的时段内的速度是 米/时. 6小时甲队铺设彩色道砖的长度是 米,乙队铺设彩色道砖的长度是 米.
(2)如果铺设的彩色道砖的总长度为150米,开挖6小时后,甲队、乙队均增加人手,提高了工作效率,此后乙队平均每小时比甲队多铺5米,结果乙反而比甲队提前1小时完成总铺设任务.求提高工作效率后甲队、乙队每小时铺设的长度分别为多少米?
参考答案:
【答案】(1)10, 5, 60, 50;(2)提高工作效率后甲队每小时铺设的长度分别为15米、乙队每小时铺设的长度为20米.
【解析】
(1)根据函数图象,速度=路程÷时间,即可解答;
(2)根据题意列方程解答即可.
解:(1)(1)由图象可得,
甲队在0≤x≤6的时段内的速度是:60÷6=10(米/时);
乙队在2≤x≤6的时段内的速度是:(5030)÷(62)=5(米/时);
6小时甲队铺设彩色道砖的长度是60米,乙队铺设彩色道砖的长度是50米.
故答案为:10;5;60;50;
(2)设提高工作效率后甲队每小时铺设的长度分别为![]() 米,由题意得:
米,由题意得:
![]() ,
,
整理得:![]() ,
,
解得:![]() ,
, ![]()
经检验:![]() ,
,![]() 都是原方程的解,
都是原方程的解,![]() 不合题意,舍去.
不合题意,舍去.
答:提高工作效率后甲队每小时铺设的长度分别为15米、乙队每小时铺设的长度为20米.
-
科目: 来源: 题型:
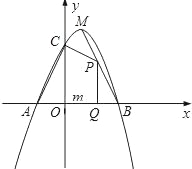
查看答案和解析>>【题目】如图,已知二次函数y=﹣x2+bx+c(c>0)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3,顶点为M.
(1)求二次函数的解析式;
(2)点P为线段BM上的一个动点,过点P作x轴的垂线PQ,垂足为Q,若OQ=m,四边形ACPQ的面积为S,求S关于m的函数解析式,并写出m的取值范围;
(3)探索:线段BM上是否存在点N,使△NMC为等腰三角形?如果存在,求出点N的坐标;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a是最大的负整数,b是-5的相反数,c=-|-2|,且a、b、c分别是点A、B、C在数轴上对应的数.
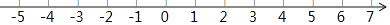
(1)求a、b、c的值,并在数轴上标出点A、B、C.
(2)若动点P从点A出发沿数轴正方向运动,动点Q同时从点B出发也沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒1个单位长度,求运动几秒后,点P可以追上点Q?
(3)在数轴上找一点M,使点M到A、B、C三点的距离之和等于12,请求出所有点M对应的数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c(a≠0)过以下三个点:(m,n),(m+2,2n),和(m+6,n),当抛物线上另有点的横坐标为m+4时,它的纵坐标为_____;当横坐标为m﹣2时,它的纵坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭.小明家中买了一辆小轿车,他连续记录了7天中每天行驶的路程(如表),以50km为标准,多于50km的记为“+”,不足50km的记为“﹣”,刚好50km的记为“0”.
第一天
第二天
第三天
第四天
第五天
第六天
第七天
路程(km)
﹣8
﹣11
﹣14
0
﹣16
+41
+8
(1)请求出这七天平均每天行驶多少千米;
(2)若每行驶100km需用汽油6升,汽油价6.2元/升,请估计小明家一个月(按30天计)的汽油费用是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司在11月11日这一天,上午卖出某品牌手机75部,下午又卖出100部,已知每部手机的售价为a元,每部手机的成本为b元.
(1)求这一天该公司卖出该品牌手机的总销售额.
(2)求这一天该公司卖出该品牌手机所得的利润.
(3)当a=6800,b=2700时,总销售额和利润分别是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,点C在半圆外,AC,BC与半圆交于D点和E点.
(1)请只用无刻度的直尺作出△ABC的两条高线,并写出作法;
(2)若AC=AB,连接DE,BE,求证:DE=BE.

相关试题

