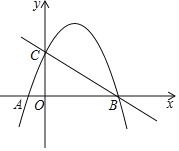
【题目】抛物线![]() 经过点A(-1,0)、B(4,0),与y轴交于点C(0,4).
经过点A(-1,0)、B(4,0),与y轴交于点C(0,4).
(1)求抛物线的表达式;
(2)点P为直线BC上方抛物线的一点,分别连接PB、PC,若直线BC恰好平分四边形COBP的面积,求P点坐标;
(3)在(2)的条件下,是否在该抛物线上存在一点Q,该抛物线对称轴上存在一点N,使得以A、P、Q、N为顶点的四边形为平行四边形?若存在,求出Q点坐标,若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)点P坐标为(2,6);(3)Q点坐标为(
;(2)点P坐标为(2,6);(3)Q点坐标为(![]() ,-
,-![]() )或(
)或(![]() ,
,![]() ).
).
【解析】(1)把A、B、C三点坐标代入抛物线y=ax2+bx+c中,求出a、b、c的值即可;
(2)设P点坐标为(x,-x2+3x+4),根据四边形COBP的面积=S△COP+ S△BOP以及四边形COBP的面积=2S△COB求解即可;
(3)分AQ和AN分别为对角线时进行讨论可得解.
(1)把A(-1,0)、B(4,0)、C(0,4)三点坐标代入抛物线y=ax2+bx+c得,
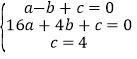 ,
,
解得: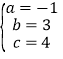
故抛物线的表达式为:y=-x2+3x+4;
(2)设P点坐标为(x,-x2+3x+4),如图,
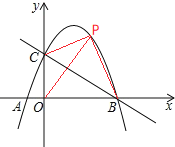
∴四边形COBP的面积=S△COP+ S△BOP=![]() =-2x2+8x+8
=-2x2+8x+8
∵直线BC平分四边形COBP的面积
∴四边形COBP的面积=2S△COB
即:-2x2+8x+8=![]()
解得x=2
将x=2代入抛物线表达式得y=6
故点P坐标为(2,6)
(3)存在
①当AQ为平行四边形的对角线时,Q点横坐标为![]() ,
,![]()
故Q(![]() )
)
②当AN为平行四边形的对角线时,Q点横坐标为![]() ,
,![]()
故Q(![]() )
)
综上所述,Q点坐标为(![]() )或(
)或(![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB为⊙O的直径,点E在⊙O上,∠EAB的平分线交⊙O于点C,过点C作AE的垂线,垂足为D,直线DC与AB的延长线交于点P.

(1)判断直线PC与⊙O的位置关系,并说明理由;
(2)若tan∠P=
 ,AD=6,求线段AE的长.
,AD=6,求线段AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,点E、N在BC上,则∠EAN=_____.
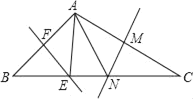
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列各题.
(1)探究:如图,
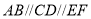 ,试说明
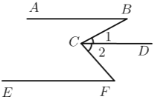
,试说明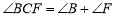 .
.
(2)拓展:如图,
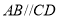 ,
,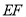 与
与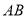 交于点
交于点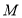 ,
,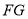 与
与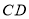 交于点
交于点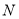 .若
.若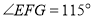 ,
,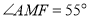 ,利用探究结论求
,利用探究结论求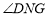 的度数.
的度数.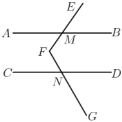
(3)应用:如图,
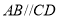 ,点
,点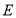 在
在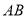 上,点
上,点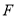 在
在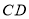 上,点
上,点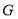 、
、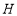 在
在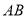 与
与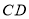 之间,
之间,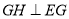 于点
于点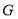 .若
.若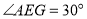 ,
,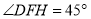 ,则
,则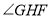 的大小为______度.
的大小为______度.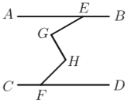
-
科目: 来源: 题型:
查看答案和解析>>【题目】保护环境,让我们从垃圾分类做起.某区环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况(如下图),进行整理后,绘制了如下两幅尚不完整的统计图:
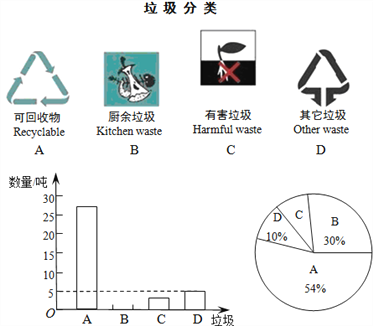
根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在扇形统计图中,求出“D”部分所对应的圆心角等于 度;
(3)在抽样数据中,产生的有害垃圾共有 吨;
(4)调查发现,在可回收物中废纸垃圾约占
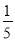 ,若每回收1吨废纸可再造纸0.85吨.假设该城市每月产生的生活垃圾为10000吨,且全部分类处理,那么每月回收的废纸可再造纸多少吨?
,若每回收1吨废纸可再造纸0.85吨.假设该城市每月产生的生活垃圾为10000吨,且全部分类处理,那么每月回收的废纸可再造纸多少吨? -
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机小王星期天上午营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天上午所接八位乘客的行车里程(单位:
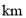 ):-3,+6,-1,-2,+4,-2,+5,-4.
):-3,+6,-1,-2,+4,-2,+5,-4.问:(1)将最后一位乘客送到目的地时,小王在什么位置?
(2)若汽车耗油量为
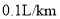 ,这天上午小王接送乘客,出租车共耗油多少升?
,这天上午小王接送乘客,出租车共耗油多少升?(3)若出租车的起步价为8元,起步里程为
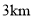 (包括
(包括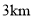 ),超过部分每千米1.5元,则小王这天上午共得车费多少元?
),超过部分每千米1.5元,则小王这天上午共得车费多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】小敏家2017年和2018年的家庭支出如下:
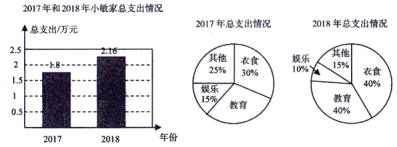
(1)2017年教育方面支出所占的百分比是多少?教育方面支出的金额是多少?
(2)2018年教育方面支出的金额是多少?教育方面支出对应的扇形圆心角度数是多少?
(3)2018年教育方面支出的金额比2017年增加了还是减少了?变化了多少?
相关试题

