【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标(4,0),其部分图象如图所示,下列结论:①抛物线过原点;②a﹣b+c<0;③4a+b+c=0;④抛物线的顶点坐标为(2,b);⑤当x<1时,y随x增大而增大.其中结论正确的是( )
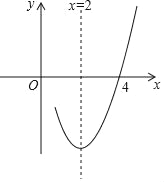
A. ①②③ B. ①④⑤ C. ①③④ D. ③④⑤
参考答案:
【答案】C
【解析】∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标(4,0),
∴抛物线与x轴的另一个交点为(0,0),故①正确,
当x=﹣1时,y=a﹣b+c>0,故②错误,
∵![]() ,得4a+b=0,b=﹣4a,
,得4a+b=0,b=﹣4a,
∵抛物线过点(0,0),则c=0,
∴4a+b+c=0,故③正确,
∴y=ax2+bx=a(x+![]() )2﹣
)2﹣![]() =a(x+
=a(x+![]() )2﹣
)2﹣![]() =a(x﹣2)2﹣4a=a(x﹣2)2+b,
=a(x﹣2)2﹣4a=a(x﹣2)2+b,
∴此函数的顶点坐标为(2,b),故④正确,
当x<1时,y随x的增大而减小,故⑤错误,
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在数轴上A点表示数
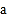 ,B点表示数
,B点表示数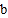 ,
,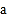 、
、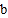 满足|
满足|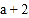 |+|
|+|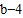 |=0;
|=0;
(1)点A表示的数为_____;点B表示的数为_____;
(2)若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),
①当t=1时,甲小球到原点的距离=_____;乙小球到原点的距离=_____.
当t=3时,甲小球到原点的距离=_____;乙小球到原点的距离=_____.
②试探究:甲,乙两小球到原点的距离可能相等吗?若不能,请说明理由.若能,请直接写出甲,乙两小球到原点的距离相等时经历的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AD=80cm,AB=40cm,半径为8cm的⊙O在矩形内且与AB、AD均相切.现有动点P从A点出发,在矩形边上沿着A→B→C→D的方向匀速移动,当点P到达D点时停止移动;⊙O在矩形内部沿AD向右匀速平移,移动到与CD相切时立即沿原路按原速返回,当⊙O回到出发时的位置(即再次与AB相切)时停止移动.已知点P与⊙O同时开始移动,同时停止移动(即同时到达各自的终止位置).当⊙O到达⊙O1的位置时(此时圆心O1在矩形对角线BD上),DP与⊙O1恰好相切,此时⊙O移动了( )cm.
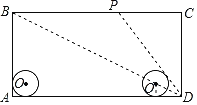
A.56B.72C.56或72D.不存在
-
科目: 来源: 题型:
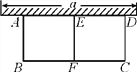
查看答案和解析>>【题目】如图,有长为24 m的篱笆,一面利用墙(墙的最大可用长度a为10 m)围成中间隔着一道篱笆的长方形花圃.
(1)现要围成面积为45 m2的花圃,则AB的长是多少米?
(2)现要围成面积为48 m2的花圃能行吗?若能行,则AB的长是多少?若不能行,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】儿童服装店老板以50元的价格购进20件衣服,针对不同的顾客,20件衣服的售价不完全相同,若以68元为标准,将超出的钱数记为正,不足的钱数记为负,记录结果如下表:
售出件数
5
4
2
1
7
1
售价
+2
+3
+1
0
—2
—1
(1)问该服装店售完这20件衣服后,赚了多少钱?
(2)老板为了促销,对购买价格不低于标准的每个顾客送了价值5元的小礼物,如果不考虑其他因素,这20件衣服实际赚了多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察算式:
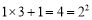 ;
;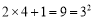 ;
;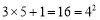 ;
;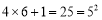 ,...请根据你发现的规律填空:
,...请根据你发现的规律填空:(1)
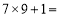 _________.
_________.(2)用含n 的等式表示上面的规律:__________.
(3)用找到的规律解决下面的问题:计算:
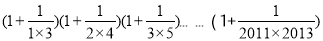 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】中华文化,源远流长,在文学方面,《西游记》《三国演义》《水浒传》《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查.根据调查结果绘制成如所示的两个不完整的统计图,请结合图中信息解决下列问题:
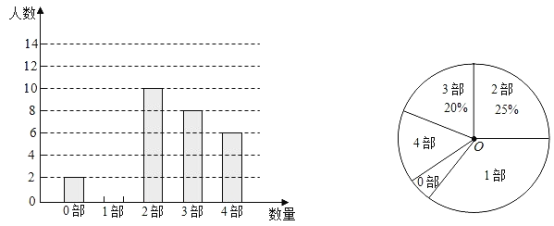
(1)请补全条形分布直方图,本次调查一共抽取了 名学生;
(2)扇形统计图中“1部”所在扇形的圆心角为 度;
(3)若该中学有1000名学生,请估计至少阅读3部四大古典名著的学生有多少名?
相关试题

