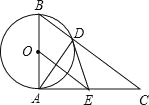
【题目】如图，已知⊙O的直径为AB，AC⊥AB于点A，BC与⊙O相交于点D，在AC上取一点E，使得ED=EA．

（1）求证：ED是⊙O的切线；

（2）当OE=10时，求BC的长．

参考答案：

【答案】(1)详见解析；（2）20.

【解析】

试题分析：（1）如图，连接OD．通过证明△AOE≌△DOE得到∠OAE=∠ODE=90°，易证得结论；（2）利用圆周角定理和垂径定理推知OE∥BC，所以根据平行线分线段成比例求得BC的长度即可．

试题解析：（1）证明：如图，连接OD．

∵AC⊥AB，

∴∠BAC=90°，即∠OAE=90°．

在△AOE与△DOE中，

，

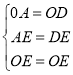∴△AOE≌△DOE（SSS），

∴∠OAE=∠ODE=90°，即OD⊥ED．

又∵OD是⊙O的半径，

∴ED是⊙O的切线；

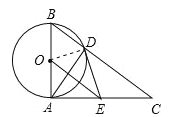
（2）解：如图，∵OE=10．

∵AB是直径，

∴∠ADB=90°，即AD⊥BC．

又∵由（1）知，△AOE≌△DOE，

∴∠AEO=∠DEO，

又∵AE=DE，

∴OE⊥AD，

∴OE∥BC，

∴，

∴BC=2OE=20，即BC的长是20．

关闭