【题目】如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数关系图象.
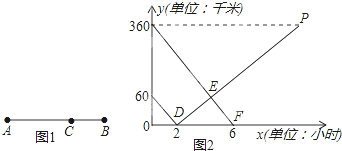
(1)填空:A,B两地相距 千米;货车的速度是 千米/时.
(2)求两小时后,货车离C站的路程y2与行驶时间x之间的函数表达式;
(3)客、货两车何时相遇?
参考答案:
【答案】(1)A,B两地相距420千米;货车的速度是30千米/时;(2)y2=30x﹣60;(3)客、货两车在出发后![]() 小时相遇.
小时相遇.
【解析】
试题分析:(1)由题意可知:B、C之间的距离为60千米,货车行驶2小时,A、C之间的距离为360千米,所以A,B两地相距360+60=420千米;
(2)根据货车两小时到达C站,求得货车的速度,进一步求得到达A站的时间,进一步设y2与行驶时间x之间的函数关系式可以设x小时到达C站,列出关系式,代入点求得函数解析式即可;
(3)两函数的图象相交,说明两辆车相遇,求得y1的函数解析式,与(2)中的函数解析式联立方程,解决问题.
解:(1)A,B两地相距420千米;货车的速度是30千米/时 …(2分)
(2)设2小时后,货车离C站的路程y2与行驶时间x之间的函数表达式为y2=kx+b,根据题意得
360÷30=12(h),12+2=14(h)
∴点P的坐标为(14,360)…(3分)
将点D(2,0)、点P(14,360)代入y2=kx+b中,![]() …(5分)
…(5分)
解得 k=30,b=﹣60
∴y2=30x﹣60…(6分)
(3)设客车离C站的路程y1与行驶时间x之间的函数表达式为y1=k1x+b1,
根据题意得
![]()
解得k1=﹣60,b1=360
y1=﹣60x+360
由y1=y2得
30x﹣60=﹣60x+360
解得x=![]()
答:客、货两车在出发后![]() 小时相遇.
小时相遇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一种童装,平均每天可售出20件,每件盈利40元。经市场调查发现,若每件降价1元,则平均每天可多售2件。该商场要保证每天盈利1200元,同时又使顾客得到实惠,那么每件应降价多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列等式正确的是( )
A. -︱3︱=︱-3︱ B. ︱3︱=︱-3︱
C. ︱-3︱=-3 D. -﹙-3﹚=-︱-3︱
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平整的地面上,有若干个完全相同棱长的小正方体堆成一个几何体,如图所示.
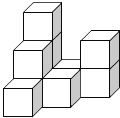
(1)请画出这个几何体的三视图.
(2)如果在这个几何体的表面喷上黄色的漆,则在所有的小正方体中,有 个正方体只有一个面是黄色,有 个正方体只有两个面是黄色,有 个正方体只有三个面是黄色.
(3)若现在你手头还有一些相同的小正方体,如果保持俯视图和左视图不变,最多可以再添加几个小正方体?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. 5x﹣3x=2 B. 2a+3b=5ab C. 2ab﹣ba=ab D. ﹣(a﹣b)=b+a
-
科目: 来源: 题型:
查看答案和解析>>【题目】若﹣7xay3+x2yb=﹣6x2y3,则a+b=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
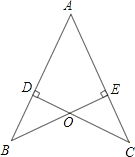
(1)求证:AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
相关试题

