【题目】如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
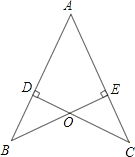
(1)求证:AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
参考答案:
【答案】(1)见解析;(2)OA⊥BC且平分BC.
【解析】
试题分析:(1)根据全等三角形的判定方法,证明△ACD≌△ABE,即可得出AD=AE,
(2)根据已知条件得出△ADO≌△AEO,得出∠DAO=∠EAO,即可判断出OA是∠BAC的平分线,即OA⊥BC.
(1)证明:在△ACD与△ABE中,
∵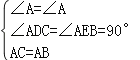 ,
,
∴△ACD≌△ABE,
∴AD=AE.
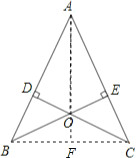
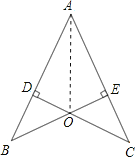
(2)答:直线OA垂直平分BC.
理由如下:连接BC,AO并延长交BC于F,
在Rt△ADO与Rt△AEO中,
![]()
∴Rt△ADO≌Rt△AEO(HL),
∴∠DAO=∠EAO,
即OA是∠BAC的平分线,
又∵AB=AC,
∴OA⊥BC且平分BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数关系图象.
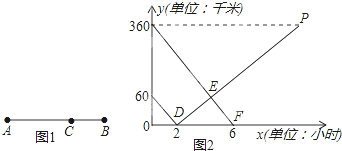
(1)填空:A,B两地相距 千米;货车的速度是 千米/时.
(2)求两小时后,货车离C站的路程y2与行驶时间x之间的函数表达式;
(3)客、货两车何时相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. 5x﹣3x=2 B. 2a+3b=5ab C. 2ab﹣ba=ab D. ﹣(a﹣b)=b+a
-
科目: 来源: 题型:
查看答案和解析>>【题目】若﹣7xay3+x2yb=﹣6x2y3,则a+b=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解中学生获取资讯的主要渠道,设置“A:手机,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项)的调查问卷,先随机抽取50名中学生进行该问卷调查,则该调查的方式是_______.(填普查或抽样调查)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠A=40°,∠B= 时,△ABC是等腰三角形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=20°,∠AOE=100°,OB平分∠AOC,OD平分∠AOE.
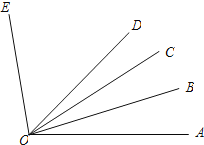
(1)求∠COD的度数;
(2)若以O为观察中心,OA为正东方向,射线OD的方向角是 ;
(3)若∠AOE的两边OA、OE分别以每秒5°、每秒3°的速度,同时绕点O逆时针方向旋转,当OA回到原处时,OA、OE停止运动,则经过几秒,∠AOE=42°.
相关试题

