【题目】如图,点C在线段AB上,AC=16cm,CB=12cm,点M、N分别是AC、BC的中点.![]()
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由.
(3)若C在线段AB的延长线上,且满足AC﹣BC=b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,不要说明理由.
参考答案:
【答案】
(1)解:∵点M、N分别是AC、BC的中点,
∴MC= ![]() AC=
AC= ![]() ×8cm=4cm,NC=
×8cm=4cm,NC= ![]() BC=
BC= ![]() ×6cm=3cm,
×6cm=3cm,
∴MN=MC+NC=4cm+3cm=7cm
(2)解:MN= ![]() acm.理由如下:
acm.理由如下:
∵点M、N分别是AC、BC的中点,
∴MC= ![]() AC,NC=
AC,NC= ![]() BC,
BC,
∴MN=MC+NC= ![]() AC+
AC+ ![]() BC=
BC= ![]() AB=
AB= ![]() acm
acm
(3)解:如图,
![]()
∵点M、N分别是AC、BC的中点,
∴MC= ![]() AC,NC=
AC,NC= ![]() BC,
BC,
∴MN=MC﹣NC= ![]() AC﹣
AC﹣ ![]() BC=
BC= ![]() (AC﹣BC)=
(AC﹣BC)= ![]() bcm.
bcm.
【解析】(1)根据点M、N分别是AC、BC的中点,得到MC=![]() AC,NC=
AC,NC=![]() BC,求出MN=MC+NC;(2)由(1)可知,C为线段AB上任一点,都能满足MN=
BC,求出MN=MC+NC;(2)由(1)可知,C为线段AB上任一点,都能满足MN=![]() acm;(3)根据题意,得到MN=MC﹣NC=
acm;(3)根据题意,得到MN=MC﹣NC=![]() bcm.
bcm.
【考点精析】根据题目的已知条件,利用线段长短的计量的相关知识可以得到问题的答案,需要掌握度量法:即用一把刻度量出两条线段的长度再比较;叠合法:从“形”的角度比较,观察点的位置.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直角三角形ABC中,∠B=90°,AB=8,BC=6,BM为中线,△BMN为等腰三角形(点N在三角形AB或AC边上,且不与顶点重合),求S△BMN .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了掌握我校初中二年级女同学身高情况,从中抽测了60名女同学的身高,这个问题中的总体是____________________,样本是____________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(﹣3,4),B(﹣4,2),C(﹣2,1),△ABC绕原点逆时针旋转90°,得到△A1B1C1,△A1B1C1向右平移6个单位,再向上平移2个单位得到△A2B2C2.
(1)画出△A1B1Cl和△A2B2C2;
(2)P(a,b)是△ABC的AC边上一点,△ABC经旋转、平移后点P的对应点分别为P1、P2,请写出点P1、P2的坐标.
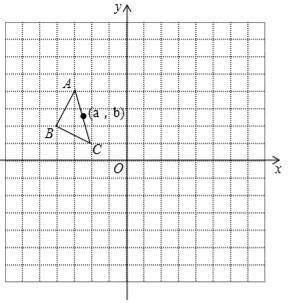
-
科目: 来源: 题型:
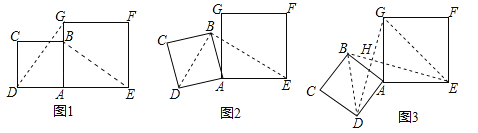
查看答案和解析>>【题目】在数学兴趣小组活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为
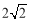 的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.(1)小明发现DG⊥BE,请你帮他说明理由;
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长;
(3)如图3,小明将正方形ABCD绕点A继续逆时针旋转,线段DG与线段BE将相交,交点为H,写出△GHE与△BHD面积之和的最大值,并简要说明理由.
-
科目: 来源: 题型:
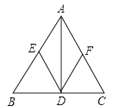
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC于D,点D,E,F分别是BC,AB,AC的中点.求证:四边形AEDF是菱形.
相关试题

