【题目】对于某一函数,给出如下定义:若存在实数![]() ,对于一函数任意的函数值
,对于一函数任意的函数值![]() ,函数值都满足
,函数值都满足![]() ,则称这个函数是有界函数,同时进一步规定,对某个有界函数,在所有满足条件的
,则称这个函数是有界函数,同时进一步规定,对某个有界函数,在所有满足条件的![]() 中,其最小值称为这个有界函数的确界值.例如如图所示的函数是有界函数,其确界值是1.5.
中,其最小值称为这个有界函数的确界值.例如如图所示的函数是有界函数,其确界值是1.5.
问:将有界函数![]() +
+![]()
![]() 的图象向上平移
的图象向上平移![]() 个单位,得到的新函数的确界值是
个单位,得到的新函数的确界值是![]() ,当
,当![]() 在什么范围时,满足
在什么范围时,满足![]() .
.
参考答案:
【答案】![]() 和
和![]() .
.
【解析】分析:需要分类讨论: ![]() ,
, ![]() ,
, ![]() 三种情况.函数向上平移m个单位后,分别求出此时确界值,再判断题意是否相符,得到结论即可.
三种情况.函数向上平移m个单位后,分别求出此时确界值,再判断题意是否相符,得到结论即可.
本题解析:
(1)若![]() , 则
, 则![]() .
.
从而, ![]()
此时,函数最值为:最大值![]() ,最小值
,最小值![]() .
.
向上平移![]() 个单位后,最值变为:最大值
个单位后,最值变为:最大值![]() ,最小值
,最小值![]() .
.
∵前者正,后者负,且后者绝对值大
∵此时该函数确界为![]() ,按确界要求,
,按确界要求, ![]() .
.
解得: ![]() .
.
.(2)若![]() , 则
, 则![]() .
.
从而, ![]() .
.
此时,函数最值为:最大值![]() ,最小值
,最小值![]() .
.
向上平移![]() 个单位后,最值变为:最大值
个单位后,最值变为:最大值![]() ,最小值
,最小值![]() .
.
∵前者正,后者负,且前者绝对值大
![]() 此时该函数确界为
此时该函数确界为![]() .
.
按确界要求, ![]() .
.
解得: ![]() .
.
.(3)若![]() , 则
, 则![]() . 从而
. 从而![]() .
.
此时最大值为![]() .平移后最大值为
.平移后最大值为![]() .
.
![]() ,
, ![]() .
.
此时函数最大值超过1, 该部分![]() 为空集.
为空集.
综上所述: ![]() 的范围为
的范围为![]() 和
和![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果用(7,3)表示七年级三班,那么八年级二班可表示成____________.
-
科目: 来源: 题型:
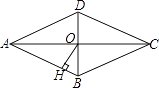
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC、BD相交于点O,且AC=8,BD=6,过点O作OH丄AB,垂足为H,则菱形的面积为 , 点O到边AB的距离OH= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一种长方体集装箱,其内空长为5米,集装箱截面的高4.5米,宽3.4米,用这样的集装箱运长为5米,横截面的外圆直径为0.8米的圆柱形钢管,为了尽可能多运,排的方案是:圆柱长5米放置于集装箱内空长,圆柱两底面放置于集装箱截面,截面的排法是:
A. 横排,每行分别为4、3、4、3、4、3
B. 横排,每行分别为4、4、4、4、4、3
C. 竖排,每列分别为5、4、5、4、5
D. 竖排,每列分别为5、5、5、5、4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在线段AB中,已知AD=2,DF=6,FB=1,有人想把线段
 分成三段:
分成三段:  、EG、GC,使得
、EG、GC,使得 :EG:GC=2:6:1,他把线段AB移到
:EG:GC=2:6:1,他把线段AB移到 的位置(即把A移到
的位置(即把A移到 ,把B移到
,把B移到 ),连接
),连接 ,分别过
,分别过 、
、 作
作 ∥
∥ ∥
∥ .
.(1)若
 =4.5,则EG= ,
=4.5,则EG= ,  = ;
= ;(2)上述方法启发我们可以解决下列问题:如图2,已知△ABC和线段a,请用直尺与圆规作
 ,满足:
,满足:①
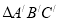 ∽△ABC;
∽△ABC;②
 的周长等于线段a的长度.(保留作图痕迹,并写出作图步骤)
的周长等于线段a的长度.(保留作图痕迹,并写出作图步骤)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a﹣(b﹣c)=a﹣b﹣c
B.a﹣(b﹣c)=a+b﹣c
C.a﹣(b﹣c)=a+b+c
D.a﹣(b﹣c)=a﹣b+c -
科目: 来源: 题型:
查看答案和解析>>【题目】李老师家距学校1900米,某天他步行去上班,走到路程的一半时发现忘带手机,此时离上班时间还有23分钟,于是他立刻步行回家取手机,随后骑电瓶车返回学校.已知李老师骑电瓶车到学校比他步行到学校少用20分钟,且骑电瓶车的平均速度是步行速度的5倍,李老师到家开门、取手机、启动电瓶车等共用4分钟.
(1)求李老师步行的平均速度;
(2)请你判断李老师能否按时上班,并说明理由.
相关试题

