【题目】新定义函数:在y关于x的函数中,若0≤x≤1时,函数y有最大值和最小值,分别记ymax和ymin , 且满足 ![]() ,则我们称函数y为“三角形函数”.
,则我们称函数y为“三角形函数”.
(1)若函数y=x+a为“三角形函数”,求a的取值范围;
(2)判断函数y=x2﹣ ![]() x+1是否为“三角形函数”,并说明理由;
x+1是否为“三角形函数”,并说明理由;
(3)已知函数y=x2﹣2mx+1,若对于0≤x≤1上的任意三个实数a,b,c所对应的三个函数值都能构成一个三角形的三边长,则求满足条件的m的取值范围.
参考答案:
【答案】
(1)
解:∵当x=0,ymin=a;x=1,ymax=1+a,
∵y=x+a为三角形函数,
∴ ![]() ,
,
∴a>1;
(2)
解:是三角形函数,理由如下:
∵对称轴为直线 ![]() ,0≤x≤1,
,0≤x≤1,
∴当 ![]() ,
,
∴ ![]() ,
,
∴它是三角形函数;
(3)
解:∵对于0≤x≤1上的任意三个实数a,b,c所对应的三个函数值都能构成一个三角形的三边长,
∴ ![]() ,若a为最小,c为最大,则有
,若a为最小,c为最大,则有 ![]() ,同理当b为最小,c为最大时也可得
,同理当b为最小,c为最大时也可得 ![]() ,
,
∴y=x2﹣2mx+1是三角形函数,
∵y=x2﹣2mx+1=(x﹣m)2﹣m2+1,
∴对称轴为直线x=m,
①当m≤0时,当x=0,ymin=1,
当x=1,ymax=﹣2m+2,则2>﹣2m+2,解得m>0,
∴无解;
②当 ![]() ,
, ![]() ,当x=1,ymax=﹣2m+2,
,当x=1,ymax=﹣2m+2, ![]() ,
,
解得0<m<1,
∴ ![]() ;
;
③当 ![]() ,
, ![]() ,当x=0,ymax=1,则
,当x=0,ymax=1,则 ![]() ,
,
解得 ![]() ,
,
∴ ![]() ;
;
④当m>1,当x=1,ymin=﹣2m+2,x=0,ymax=1,则 ![]() ,
,
解得 ![]() ,
,
∴无解;
综上述可知m的取值范围为 ![]() 或
或 ![]() .
.
【解析】(1)由函数的性质可求得其最大值和最小值,由三角形函数的定义可得到关于a的不等式组,可求得a的取值范围;(2)由抛物线解析式可求得其对称轴,由x的范围可求得其最大值和最小值,满足三角形函数的定义;(3)由三角形的三边关系可判断函数y=x2﹣2mx+1为三角形函数,再利用三角形函数的定义分别得到关于m的不等式组,即可求得m所满足的不等式,可求得m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】重庆市中小学教育大力提倡“2+2”素质教育,在开展的几年来,取得了重大成果.小明对本学期全班50名同学所选择的活动项目进行了统计,根据收集的数据制作了下表:
1)请完善表格中的数据:

2)根据上述表格中的人数百分比,绘制合适的统计图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地电话拨号上网有两种收费方式,用户可以任选其一:
(A)计时制,0.08元/分;
(B)包月制,50元/月(限一部个人住宅电话上网);
此外,每种上网方式都附加通信费0.02元/分.
(1)某用户某月上网时间为x分钟,则该用户在A、B两种收费方式下应支付费用各多少元?
(2)如果一个月内上网200分钟和300分钟,按两种收费方式各需交费多少元?
(3)是否存在某一时间,会出现两种收费方式一样的情况?如果存在,请求出这时的上网时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)4-
 m=-m; (2)56-8x=11+x;
m=-m; (2)56-8x=11+x;(3)
 x+1=5+
x+1=5+ x; (4)-5x+6+7x=1+2x-3+8x.
x; (4)-5x+6+7x=1+2x-3+8x. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明设计了一个问题,分两步完成:
(1)已知关于x的一元一次方程
 ,请画出数轴,并在数轴上标注a与
,请画出数轴,并在数轴上标注a与 对应的点,分别记作A,B;
对应的点,分别记作A,B;(2)在第1问的条件下,在数轴上另有一点C对应的数为y,C与A的距离是C与B的距离的5倍,且C在表示5的点的左侧,求y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为 __________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆形纸片⊙O的直径为2,将其沿着两条互相垂直的直径折叠,得到四层的扇形,将最上的一层“撑”开来,“鼓”成一个无底的圆锥,则这个圆锥的高是( )

A.
B.
C.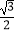
D.1
相关试题

