【题目】如图所示,已知点M(0,2),直线y= ![]() x+4与两坐标轴分别交于A,B两点,P、Q分别是线段OA,AB上的动点,则PQ+MP的最小值是 .
x+4与两坐标轴分别交于A,B两点,P、Q分别是线段OA,AB上的动点,则PQ+MP的最小值是 . 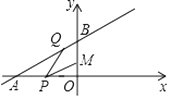
参考答案:
【答案】3 ![]()
【解析】解:如图,点M关于x轴的对称点N(0,﹣2),过点N作NQ⊥AB交OA于P,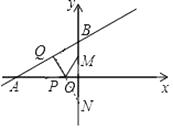
则NQ=PQ+PM的最小值,
∵直线y= ![]() x+4与两坐标轴分别交于A,B两点,
x+4与两坐标轴分别交于A,B两点,
∵B(0,4),∠OAB=30°,
∴∠ABO=60°,BN=4+2=6,
∴在Rt△BQN中,QN=sin60°BN=3 ![]() ,
,
∴PM+MN的最小值是 3 ![]() .
.
所以答案是 3 ![]() .
.
【考点精析】本题主要考查了一次函数的性质和一次函数的图象和性质的相关知识点,需要掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】骰子是一种特别的数字立方体(见右图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( )

A.
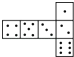 B.
B.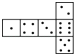 C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OABC是平行四边形,边OC在x轴的负半轴上,反比例y=
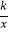 (k<0)的图象经过点A与BC的中点F,连接AF、OF,若△AOF的面积为9,则k的值为 .
(k<0)的图象经过点A与BC的中点F,连接AF、OF,若△AOF的面积为9,则k的值为 . 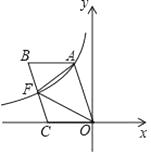
-
科目: 来源: 题型:
查看答案和解析>>【题目】饮水机原有水的温度为20℃,通电开机后,饮水机自动开始加热(此过程中水温y与开机时间x满足一次函数关系),当加热到100℃是自动停止加热,随后水温开始下降(此过程水温y与开机时间x成反比例关系),当水温将至20℃时,饮水机又自动开始加热,…重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)当0≤x≤8,求水温y与开机时间x的函数关系.
(2)求图中t的值.
(3)在通电后45分钟饮水机内水温约为多少度?在通电后60分钟饮水机内水温约为多少度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,相距5km的A、B两地间有一条笔直的马路,C地位于AB两地之间且距A地2km,小明同学骑自行车从A地出发沿马路以每小时5km的速度向B地匀速运动,当到达B地后立即以原来的速度返回。到达A地停止运动,设运动时间为t(小时).小明的位置为点P、若以点C为坐标原点,以从A到B为正方向,用1个单位长度表示1km,解答下列各问:
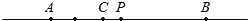
(1)指出点A所表示的有理数;
(2)求t =0.5时,点P表示的有理数;
(3)当小明距离C地1km时,直接写出所有满足条件的t值;
(4)在整个运动过程中,求点P与点A的距离(用含t的代数式表示);
(5)用含t的代数式表示点P表示的有理数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)3(20-y)=6y-4(y-11);
(2)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解本校九年级男生“引体向上”项目的训练情况,随机抽取该年级部分男生进行了一次测试(满分15分,成绩均记为整数分),并按测试成绩(单位:分)分成四类:A类(12≤m≤15),B类(9≤m≤11),C类(6≤m≤8),D类(m≤5)绘制出以下两幅不完整的统计图,请根据图中信息解答下列问题:
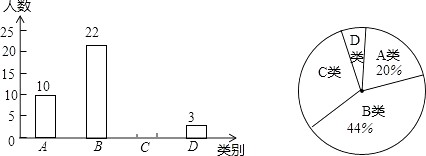
(1)本次抽取样本容量为 , 扇形统计图中A类所对的圆心角是度;
(2)请补全条形统计图;
(3)若该校九年级男生有600名,请估计该校九年级男生“引体向上”项目成绩为C类的有多少名?
相关试题

