【题目】解方程:
(1)3(20-y)=6y-4(y-11);
(2)![]()
参考答案:
【答案】(1)y=3.2;(2)x=![]() .
.
【解析】
试题(1)按照去括号,移项,合并同类项,系数化为1的步骤解答,去括号时一是不要漏乘括号内的项,二是明确括号前的符号;(2)按照去分母,去括号,移项,合并同类项,系数化为1的步骤解答,去分母一要注意不要漏乘没有分母的项,二要注意去掉分母后把分子加括号.
(1) 3(20 - y)= 6 y- 4(y-11)
去括号得, 60 – 3 y =6 y- 4y + 44
移项得, - 3 y- 2 y=44-60
合并得, -5 y = - 16
系数化为1得, y=3.2
(2)![]()
去分母得,6-(x-1)=2(3x-1),
去括号得, 6-x+1=6x-2,
移项得, -x-6x=-2-6-1,
合并得, -7x=-9
化系数为1得, x=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】饮水机原有水的温度为20℃,通电开机后,饮水机自动开始加热(此过程中水温y与开机时间x满足一次函数关系),当加热到100℃是自动停止加热,随后水温开始下降(此过程水温y与开机时间x成反比例关系),当水温将至20℃时,饮水机又自动开始加热,…重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)当0≤x≤8,求水温y与开机时间x的函数关系.
(2)求图中t的值.
(3)在通电后45分钟饮水机内水温约为多少度?在通电后60分钟饮水机内水温约为多少度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知点M(0,2),直线y=
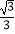 x+4与两坐标轴分别交于A,B两点,P、Q分别是线段OA,AB上的动点,则PQ+MP的最小值是 .
x+4与两坐标轴分别交于A,B两点,P、Q分别是线段OA,AB上的动点,则PQ+MP的最小值是 . 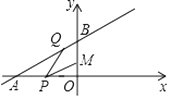
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,相距5km的A、B两地间有一条笔直的马路,C地位于AB两地之间且距A地2km,小明同学骑自行车从A地出发沿马路以每小时5km的速度向B地匀速运动,当到达B地后立即以原来的速度返回。到达A地停止运动,设运动时间为t(小时).小明的位置为点P、若以点C为坐标原点,以从A到B为正方向,用1个单位长度表示1km,解答下列各问:
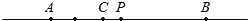
(1)指出点A所表示的有理数;
(2)求t =0.5时,点P表示的有理数;
(3)当小明距离C地1km时,直接写出所有满足条件的t值;
(4)在整个运动过程中,求点P与点A的距离(用含t的代数式表示);
(5)用含t的代数式表示点P表示的有理数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解本校九年级男生“引体向上”项目的训练情况,随机抽取该年级部分男生进行了一次测试(满分15分,成绩均记为整数分),并按测试成绩(单位:分)分成四类:A类(12≤m≤15),B类(9≤m≤11),C类(6≤m≤8),D类(m≤5)绘制出以下两幅不完整的统计图,请根据图中信息解答下列问题:
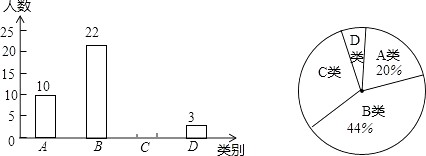
(1)本次抽取样本容量为 , 扇形统计图中A类所对的圆心角是度;
(2)请补全条形统计图;
(3)若该校九年级男生有600名,请估计该校九年级男生“引体向上”项目成绩为C类的有多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】在四张背面完全相同的纸牌A、B、C、D中,其中正面分别画有四个不同的几何图形(如图),小华将这4张纸牌背面朝上洗匀后摸出一张(不放回),再从余下的3张纸牌中摸出一张.
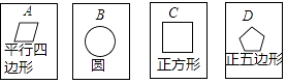
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张纸牌牌面上所画几何图形,既是轴对称图形又是中心对称图形的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小华在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进30米到达C处,又测得顶部E的仰角为60°,求大楼EF的高度.(结果精确到0.1米,参考数据
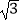 =1.732)
=1.732)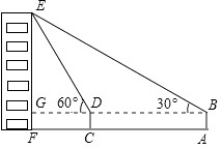
相关试题

