【题目】如图,四边形OABC是平行四边形,边OC在x轴的负半轴上,反比例y= ![]() (k<0)的图象经过点A与BC的中点F,连接AF、OF,若△AOF的面积为9,则k的值为 .
(k<0)的图象经过点A与BC的中点F,连接AF、OF,若△AOF的面积为9,则k的值为 . 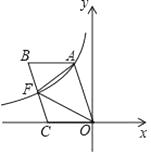
参考答案:
【答案】-9
【解析】解:∵△AOF的面积为9,四边形OABC是平行四边形, ∴△BOC的面积是9,
∵反比例y= ![]() (k<0)的图象经过点A与BC的中点F,
(k<0)的图象经过点A与BC的中点F,
∴△OCF的面积是4.5,
∵点F在反比例函数y= ![]() (k<0)的图象上,
(k<0)的图象上,
∴k=﹣(4.5×2)=﹣9,
所以答案是:﹣9.
【考点精析】利用比例系数k的几何意义和平行四边形的性质对题目进行判断即可得到答案,需要熟知几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=10,BC=8,P为AD的中点,将△ABP沿BP翻折至△EBP(点A落到点E处),连接DE,则图中与∠APB相等的角的个数为( )
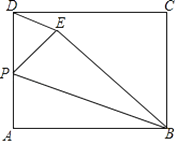
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD∶AB=__________时,四边形MENF是正方形(只写结论,不需证明).

-
科目: 来源: 题型:
查看答案和解析>>【题目】骰子是一种特别的数字立方体(见右图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( )

A.
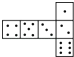 B.
B.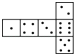 C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】饮水机原有水的温度为20℃,通电开机后,饮水机自动开始加热(此过程中水温y与开机时间x满足一次函数关系),当加热到100℃是自动停止加热,随后水温开始下降(此过程水温y与开机时间x成反比例关系),当水温将至20℃时,饮水机又自动开始加热,…重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)当0≤x≤8,求水温y与开机时间x的函数关系.
(2)求图中t的值.
(3)在通电后45分钟饮水机内水温约为多少度?在通电后60分钟饮水机内水温约为多少度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知点M(0,2),直线y=
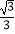 x+4与两坐标轴分别交于A,B两点,P、Q分别是线段OA,AB上的动点,则PQ+MP的最小值是 .
x+4与两坐标轴分别交于A,B两点,P、Q分别是线段OA,AB上的动点,则PQ+MP的最小值是 . 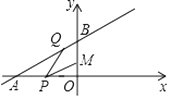
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,相距5km的A、B两地间有一条笔直的马路,C地位于AB两地之间且距A地2km,小明同学骑自行车从A地出发沿马路以每小时5km的速度向B地匀速运动,当到达B地后立即以原来的速度返回。到达A地停止运动,设运动时间为t(小时).小明的位置为点P、若以点C为坐标原点,以从A到B为正方向,用1个单位长度表示1km,解答下列各问:
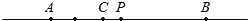
(1)指出点A所表示的有理数;
(2)求t =0.5时,点P表示的有理数;
(3)当小明距离C地1km时,直接写出所有满足条件的t值;
(4)在整个运动过程中,求点P与点A的距离(用含t的代数式表示);
(5)用含t的代数式表示点P表示的有理数.
相关试题

