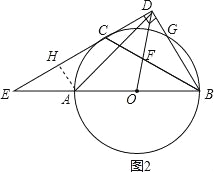
【题目】如图,AB是⊙O的直径,C、G是⊙O上两点,且C是弧AG的中点,过点C的直线CD⊥BG的延长线于点D,交BA的延长线于点E,连接BC,交OD于点F.

(1)求证:CD是⊙O的切线;
(2)若![]() ,求证:AE=AO;
,求证:AE=AO;
(3)连接AD,在(2)的条件下,若CD=2![]() ,求AD的长.
,求AD的长.
参考答案:
【答案】(1)证明见解析(2)∠E=30°;(3)![]()
【解析】
试题分析:(1)如图1,连接OC,AC,CG,由圆周角定理得到∠ABC=∠CBG,根据同圆的半径相等得到OC=OB,于是得到∠OCB=∠OBC,等量代换得到∠OCB=∠CBG,根据平行线的判定得到OC∥BG,即可得到结论;
(2)由OC∥BD,得到△OCF∽△BDF,△EOC∽△EBD,得到![]() ,
,![]() ,根据直角三角形的性质即可得到结论;
,根据直角三角形的性质即可得到结论;
(3)如图2,过A作AH⊥DE于H,解直角三角形得到BD=6,DE=6![]() ,BE=12,在Rt△DAH中,AD=
,BE=12,在Rt△DAH中,AD=![]() ,求出答案即可.
,求出答案即可.
试题解析:(1)如图1,连接OC,AC,CG,
∵AC=CG,
∴![]() ,
,
∴∠ABC=∠CBG,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠OCB=∠CBG,
∴OC∥BG,
∵CD⊥BG,
∴OC⊥CD,
∴CD是⊙O的切线;

(2)∵OC∥BD,
∴△OCF∽△BDF,△EOC∽△EBD,
∴![]() ,
,
∴![]() ,
,
∵OA=OB,
∴AE=OA=OB,
∴OC=![]() OE,
OE,
∵∠ECO=90°,
∴∠E=30°;
(3)如图2,过A作AH⊥DE于H,
∵∠E=30°
∴∠EBD=60°,
∴∠CBD=![]() ∠EBD=30°,
∠EBD=30°,
∵CD=2![]() ,
,
∴BD=6,DE=6![]() ,BE=12,
,BE=12,
∴AE=![]() BE=4,
BE=4,
∴AH=2,
∴EH=2![]() ,
,
∴DH=4![]() ,
,
在Rt△DAH中,AD=![]() =2
=2![]() .
.
-
科目: 来源: 题型:
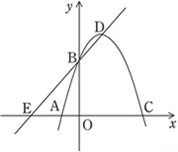
查看答案和解析>>【题目】如图(1),在平面直角坐标系中,抛物线
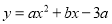 经过
经过A(-1,0)、B(0,3)两点,与
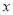 轴交于另一点C,顶点为D.
轴交于另一点C,顶点为D.(1)求该抛物线的解析式及点C、D的坐标;
(2)经过点B、D两点的直线与
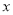 轴交于点E,若点F是抛物线上一点,以A、B、E、F为顶点的四边形是平行四边形,求点F的坐标;
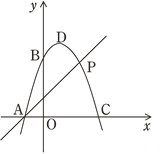
轴交于点E,若点F是抛物线上一点,以A、B、E、F为顶点的四边形是平行四边形,求点F的坐标;(3)如图(2)P(2,3)是抛物线上的点,Q是直线AP上方的抛物线上一动点,求△APQ的最大面积和此时Q点的坐标.
图(1) 图(2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】当a
 ,
, 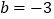 时,求多项式3(a2-2ab)-[3a2-2b+2(ab+b)]的值.
时,求多项式3(a2-2ab)-[3a2-2b+2(ab+b)]的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,要得到△ABD≌△ACD,还需从下列条件中补选一个,则错误的选法是( )
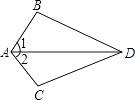
A.AB=AC
B.DB=DC
C.∠ADB=∠ADC
D.∠B=∠C -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知C是AB的中点,D是AC的中点,E是BC的中点.

(1)若AB=16cm,求DE的长;
(2)若CE=4cm,求DB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】若抛物线开口向下,且与y轴交于点(0,1),写出一个满足条件的抛物线的解析式:_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若p=x2y,则-x10y5·(-2x2y)3的计算结果是( )
A. -8p8 B. 8p8 C. -6p8 D. 6p8
相关试题

