【题目】已知在纸面上有一数轴(如图1),折叠纸面.
(1)若1表示的点与﹣1表示的点重合,则﹣4表示的点与 表示的点重合;
(2)若﹣2表示的点与8表示的点重合,回答以下问题:
①16表示的点与 表示的点重合;
②如图2,若数轴上A、B两点之间的距离为2018(A在B的左侧),且A、B两点经折叠后重合,则A、B两点表示的数分别是 、 .
(3)如图3,若m和n表示的点C和点D经折叠后重合,(m>n>0),现数轴上P、Q两点之间的距离为a(P在Q的左侧),且P、Q两点经折叠后重合,求P、Q两点表示的数分别是多少?(用含m,n,a的代数式表示)
参考答案:
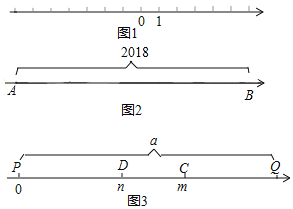
【答案】(1)4;(2)①-10;②﹣1006、1012;(3)点P表示的数为:![]() ;点Q表示的数为:
;点Q表示的数为:![]()
【解析】
(1)由表示1与﹣1的两点重合,利用对称性即可得到结果;
(2)由﹣2表示的点与8表示的点重合,确定出3为对称点,得出两项的结果即可;
(3)根据(2)的计算方法进行解答.
(1)若1表示的点与﹣1表示的点重合,则原点为对称点,所以﹣4表示的点与4表示的点重合;
(2)由题意得:(﹣2+8)÷2=3,即3为对称点,
①根据题意得:2×3﹣16=﹣10;
②∵3为对称点,A、B两点之间的距离为2018(A在B的左侧),且A、B两点经折叠后重合,
∴A表示的数=﹣![]() +3=﹣1006,B点表示的数=
+3=﹣1006,B点表示的数=![]() +3=1012;
+3=1012;
(3)点P表示的数为:![]() ;点Q表示的数为:
;点Q表示的数为:![]() .
.
故答案为:(1)4;(2)①﹣10; ②﹣1006,1012.(3)点P表示的数为:![]() ;点Q表示的数为:
;点Q表示的数为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+6与x轴、y轴分别交于点E,F,点E的坐标为(﹣8,0),点A的坐标为(﹣6,0)
(1)求k的值;
(2)若点P(x,y)是第二象限内的直线上的一个动点,在点P的运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)在(2)的条件下,探究:当点P运动到什么位置时,△OPA的面积为
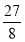 ,并说明理由;
,并说明理由;(4)问在x轴上是否存在点Q,使得△EFQ为等腰三角形?若存在,求出符合条件的Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学对多项式(a2-4a+2)(a2-4a+6)+4进行因式分解的过程:
解:设a2-4a=y,则
原式=(y+2)(y+6)+4(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(a2-4a+4)2.(第四步)
(1)该同学因式分解的结果是否彻底:________(填“彻底”或“不彻底”);
(2)若不彻底,请你直接写出因式分解的最后结果:________;
(3)请你模仿以上方法对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,∠ACB=90°,BC=2,AC=4,点D在射线BC上,以点D为圆心,BD为半径画弧交边AB于点E,过点E作EF⊥AB交边AC于点F,射线ED交射线AC于点G.
(1)求证:△EFG∽△AEG;
(2)设FG=x,△EFG的面积为y,求y关于x的函数解析式并写出定义域;
(3)联结DF,当△EFD是等腰三角形时,请直接写出FG的长度.



-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图形中每一小格正方形的边长为1,已知△ABC
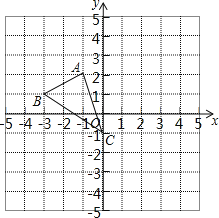
(1)AC的长等于 .(结果保留根号)
(2)将△ABC向右平移2个单位得到△A′B′C′,则A点的对应点A′的坐标是 ;
(3)画出将△ABC绕点C按顺时针方向旋转90°后得到△A1B1C1,并写出A点对应点A1的坐标?
-
科目: 来源: 题型:
查看答案和解析>>【题目】顶点都在格点上的三角形叫做格点三角形,如图,在4×4的方格纸中,△ABC是格点三角形.
(1)在图1中,以点C为对称中心,作出一个与△ABC成中心对称的格点三角形DEC,直接写出AB与DE的位置关系;
(2)在图2中,以AC所在的直线为对称轴,作出一个与△ABC成和对称的格点三角形AFC,直接写出△BCF是什么形状的特殊三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
相关试题

