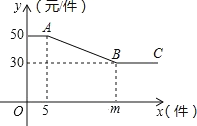
【题目】某商店经销某种玩具,该玩具每个进价 20 元,为进行促销,商店制定如下“优惠” 方案:如果一次销售数量不超过 5 个,则每个按 50 元销售:如果一次销售数量超过 5 个,则每增加一个,所有玩具均降低 1 元销售,但单价不得低于 30 元,一次销售该玩具的单价 y(元)与销售数量 x(个)之间的函数关系如下图所示.
(1)结合图形,求出 m 的值;射线 BC 所表示的实际意义是什么;
(2)求线段 AB 满足的 y 与 x 之间的函数解析式,并直接写出自变量的取值范围;
(3)当销售 15 个时,商店的利润是多少元.
参考答案:
【答案】(1)25、当一次销售数量超过 25 个时,每个均按 30 元销售;(2)线段 AB 满足的 y 与 x 之间的函数解析式是 y=-x+55(5≤x≤25);(3)此时商店的利润为300元.
【解析】
(1)根据单价不得低于30元,即可求出m,所以BC表示当销量超过 25 个时,每个均按 30 元销售,
(2)待定系数法即可求解,
(3)将x=15代入解析式中即可求解.
(1)m=5+(50-30)÷1=25 ,
射线BC 所表示的实际意义为当一次销售数量超过25 个时,每个均按 30 元销售,
故答案为:25、当一次销售数量超过 25 个时,每个均按 30 元销售;
(2)设线段 AB 满足的 y 与 x 之间的函数解析式为 y=kx+b, ![]() ,得
,得 ![]() ,
,
即线段 AB 满足的 y 与 x 之间的函数解析式是 y=-x+55(5≤x≤25);
(3)当 y=15 时,15=-x+55,得 x=40,
∴此时商店的利润为:15×[40 -20]=300(元)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+1交y轴于点A,交x轴正半轴于点B(4,0),与过A点的直线相交于另一点D(3,
 ),过点D作DC⊥x轴,垂足为C.
),过点D作DC⊥x轴,垂足为C.
(1)求抛物线的表达式;
(2)点P在线段OC上(不与点O、C重合),过P作PN⊥x轴,交直线AD于M,交抛物线于点N,连接CM,求△PCM面积的最大值;
(3)若P是x轴正半轴上的一动点,设OP的长为t,是否存在t,使以点M、C、D、N为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由. -
科目: 来源: 题型:
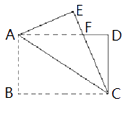
查看答案和解析>>【题目】如图,矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )
A.
B.
C.
D.
-
科目: 来源: 题型:
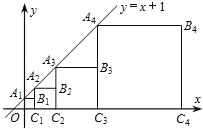
查看答案和解析>>【题目】如图,直线 y=x+1 与 y 轴交于点 A1,以 OA1为边,在 y 轴右侧作正方形 OA1B1C1,延长 C1B1交直线 y=x+1 于点 A2,再以 C1A2为边作正方形,…,这些正方形与直线 y=x+1 的交点分别为 A1,A2,A3,…,An,则点 Bn 的坐标为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在探索“尺规三等分角”这个数学名题的过程中,曾利用了如图,该图中,四边形ABCD是矩形,E是BA延长线上一点,F是CE上一点,∠ACF=∠AFC,∠FAE=∠FEA。若∠ACB=21°,则∠ECD的度数是( )

A.7°
B.21°
C.23°
D.24° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数 y=2x 与 y=ax+5 的图象相交于点 A(m,4).
(1)求 A 点坐标及一次函数 y=ax+5 的解析式;
(2)设直线 y=ax+5 与 x 轴交于点 B,求△AOB 的面积;
(3)求不等式 2x<ax+5 的解集.

-
科目: 来源: 题型:
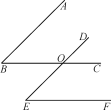
查看答案和解析>>【题目】如图,已知BC,DE相交于点O,给出以下三个判断:①AB∥DE;②BC∥EF;③∠B=∠E,请你以其中两个判断作为题设,另外一个判断作为结论,写出所有的命题,指出这些命题是真命题还是假命题,并选择其中的一个真命题加以证明.
相关试题

