【题目】如图,抛物线![]() 经过B(﹣1,0),D(﹣2,5)两点,与x轴另一交点为A,点H是线段AB上一动点,过点H的直线PQ⊥x轴,分别交直线AD、抛物线于点Q,P.
经过B(﹣1,0),D(﹣2,5)两点,与x轴另一交点为A,点H是线段AB上一动点,过点H的直线PQ⊥x轴,分别交直线AD、抛物线于点Q,P.
(1)求抛物线的解析式;
(2)是否存在点P,使∠APB=90°,若存在,求出点P的横坐标,若不存在,说明理由;
(3)连接BQ,一动点M从点B出发,沿线段BQ以每秒1个单位的速度运动到Q,再沿线段QD以每秒![]() 个单位的速度运动到D后停止,当点Q的坐标是多少时,点M在整个运动过程中用时t最少?
个单位的速度运动到D后停止,当点Q的坐标是多少时,点M在整个运动过程中用时t最少?

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)Q(﹣1,4).
;(3)Q(﹣1,4).
【解析】试题分析:(1)把B(﹣1,0),D(﹣2,5)代入![]() ,得出关于b、c的二元一次方程组,即可求出抛物线的解析式;
,得出关于b、c的二元一次方程组,即可求出抛物线的解析式;
(2)根据抛物线解析式求出OA,设P(m,m2﹣2m﹣3),则﹣1≤m≤3,PH=﹣(m2﹣2m﹣3),BH=1+m,AH=3﹣m,证明△AHP∽△PHB,得出PH2=BHAH,由此得出方程[﹣(m2﹣2m﹣3)]2=(1+m)(3﹣m),解方程即可;
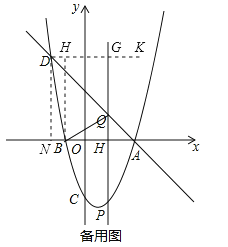
(3)由题意,动点M运动的路径为折线BQ+QD,运动时间:t=BQ+![]() DQ,如备用图,作辅助线,将BQ+
DQ,如备用图,作辅助线,将BQ+![]() DQ转化为BQ+QG;再由垂线段最短,得到垂线段BH与直线AD的交点即为所求的Q点.
DQ转化为BQ+QG;再由垂线段最短,得到垂线段BH与直线AD的交点即为所求的Q点.
试题解析:解:(1)把B(﹣1,0),D(﹣2,5)代入![]() ,得:
,得: ![]() ,解得:
,解得: ![]() ,∴抛物线的解析式为:
,∴抛物线的解析式为: ![]() ;
;
(2)存在点P,使∠APB=90°.当y=0时,即x2﹣2x﹣3=0,解得:x1=﹣1,x2=3,∴OB=1,OA=3.
设P(m,m2﹣2m﹣3),则﹣1≤m≤3,PH=﹣(m2﹣2m﹣3),BH=1+m,AH=3﹣m,∵∠APB=90°,PH⊥AB,∴∠PAH=∠BPH=90°﹣∠APH,∠AHP=∠PHB,∴△AHP∽△PHB,∴ ![]() ,∴PH2=BHAH,∴[﹣(m2﹣2m﹣3)]2=(1+m)(3﹣m),解得m1=
,∴PH2=BHAH,∴[﹣(m2﹣2m﹣3)]2=(1+m)(3﹣m),解得m1=![]() ,m2=
,m2=![]() ,∴点P的横坐标为:
,∴点P的横坐标为: ![]() 或
或![]() ;
;
(3)如图,过点D作DN⊥x轴于点N,则DN=5,ON=2,AN=3+2=5,∴tan∠DAB=![]() =1,∴∠DAB=45°.过点D作DK∥x轴,则∠KDQ=∠DAB=45°,DQ=
=1,∴∠DAB=45°.过点D作DK∥x轴,则∠KDQ=∠DAB=45°,DQ=![]() QG.
QG.
由题意,动点M运动的路径为折线BQ+QD,运动时间:t=BQ+![]() DQ,∴t=BQ+QG,即运动的时间值等于折线BQ+QG的长度值.
DQ,∴t=BQ+QG,即运动的时间值等于折线BQ+QG的长度值.
由垂线段最短可知,折线BQ+QG的长度的最小值为DK与x轴之间的垂线段.
过点B作BH⊥DK于点H,则t最小=BH,BH与直线AD的交点,即为所求之Q点.
∵A(3,0),D(﹣2,5),∴直线AD的解析式为:y=﹣x+3,∵B点横坐标为﹣1,∴y=1+3=4,∴Q(﹣1,4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解七年级学生的学习情况,在这个年级抽取了50名学生对某课进行了测试。将所得的成绩(成绩均为整数)进行整理(如下边所示),请你画出频数分布直方图和频数折线图,并回答问题:
分数





频率
0.04
0.04
0.16
0.34
0.42
 这次测试及格(包括60分)的人数有多少?
这次测试及格(包括60分)的人数有多少? 本次测试这50名学生成绩的优秀率是多少?(90分以上为优秀,包括90分)
本次测试这50名学生成绩的优秀率是多少?(90分以上为优秀,包括90分) 这个年级此学科学习情况如何?
这个年级此学科学习情况如何? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级学生进行体育测试,七年级(2)班男生的立定跳远成绩制成频数分布直方图,图中从左到右各矩形的高之比是
 ,最后一组的频数是6,根据直方图所表达的信息,解答下列问题。
,最后一组的频数是6,根据直方图所表达的信息,解答下列问题。(1)该班有多少名男生?
(2)若立定跳远的成绩在2.0米以上(包括2.0米)为合格率是多少
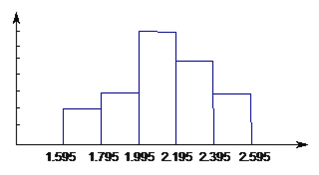
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校学生会准备调查全校七年级学生 每天(除课间操外)的课外锻炼时间。
(1)确定调查方式时,甲说:“我到(1)班去调查全体同学”;乙同学说:“我到体育场上去询问参加锻炼的同学”;丙同学说:“我到全校七年级每个班去随机调查一定数量的同学”。你认为调查方式最合理的是(填“甲”、或“乙”或“丙”)_________
(2)他们采用了最为合适的调查方法收集数据,并绘制出如图1所示的条形统计图和如图2所示的扇形统计图,请将两幅统计图补充完整;


(3)若该七年级共有1200名同学,请你估计其中每天(除课间操外)课外锻炼时间不大于20分钟的人数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】反比例函数
 (k≠0)的图象是__________,当k>0时,图象的两个分支分别在第__________、__________象限内,在每个象限内,y随x的增大而__________;当k<0时,图象的两个分支分别在第__________、__________象限内,在每个象限内,y随x的增大而__________;
(k≠0)的图象是__________,当k>0时,图象的两个分支分别在第__________、__________象限内,在每个象限内,y随x的增大而__________;当k<0时,图象的两个分支分别在第__________、__________象限内,在每个象限内,y随x的增大而__________; -
科目: 来源: 题型:
查看答案和解析>>【题目】已知y与x的部分取值满足下表:

(1)试猜想y与x的函数关系可能是你们学过的哪类函数,并写出这个函数的解析式.(不要求写x的取值范围)
(2)简要叙述该函数的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知10x=8,10y=16,则102x-y=______.
相关试题

