【题目】直角三角形![]() 中,
中,![]() ,直线
,直线![]() 过点
过点![]() .
.
(1)当![]() 时,如图1,分别过点
时,如图1,分别过点![]() 和
和![]() 作
作![]() 直线
直线![]() 于点
于点![]() ,
,![]() 直线
直线![]() 于点
于点![]() .
.![]() 与
与![]() 是否全等,并说明理由;
是否全等,并说明理由;
(2)当![]() ,
,![]() 时,如图2,点
时,如图2,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,连接
对称,连接![]() 、
、![]() .点
.点![]() 是
是![]() 上一点,点
上一点,点![]() 是
是![]() 上一点,分别过点
上一点,分别过点![]() 、
、![]() 作
作![]() 直线
直线![]() 于点
于点![]() ,
,![]() 直线
直线![]() 于点
于点![]() ,点
,点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 的速度沿
的速度沿![]() 路径运动,终点为
路径运动,终点为![]() .点
.点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 的速度沿
的速度沿![]() 路径运动,终点为
路径运动,终点为![]() .点
.点![]() 、
、![]() 同时开始运动,各自达到相应的终点时停止运动,设运动时间为
同时开始运动,各自达到相应的终点时停止运动,设运动时间为![]() 秒.
秒.
①当![]() 为等腰直角三角形时,求
为等腰直角三角形时,求![]() 的值;
的值;
②当![]() 与
与![]() 全等时,求
全等时,求![]() 的值.
的值.


图1 图2
参考答案:
【答案】(1)△ACD≌△CBE.
(2)①![]() 或5. ②当t=3.5秒或5秒或6.5秒时,△MDC≌△CEN.
或5. ②当t=3.5秒或5秒或6.5秒时,△MDC≌△CEN.
【解析】
(1)根据同角的余角相等得到∠DAC=∠ECB,根据全等三角形的判定定理证明即可;
(2)①分点N沿F→C→B路径运动、点N沿B→C路径运动两种情况进行讨论.
②分点N沿F→C路径运动、点N沿C→B路径运动、点N沿B→C路径运动、点N沿C→F路径运动四种情况计算即可.
(1)△ACD≌△CBE,
理由如下:∵![]()
∴![]()
∵AD⊥直线l,
∴![]()
∴∠DAC=∠ECB,
在△ACD和△CBE中,
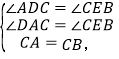
∴△ACD≌△CBE;
(2)①当![]() 为等腰直角三角形时,点N在BC上,
为等腰直角三角形时,点N在BC上,
![]()
点![]() 从点
从点![]() 出发第一次到线段CB上时,
出发第一次到线段CB上时,
![]()
![]()
![]() 解题
解题![]()
点![]() 从点
从点![]() 出发第二次到线段CB上时,
出发第二次到线段CB上时,
![]()
![]()
![]() 解题
解题![]()
②由题意得,CF=BC=6cm,
由(1)得,∠DAC=∠ECB,∠ADC=∠CEB,
∴当CM=CN时,△MDC≌△CEN,
当点N沿F→C路径运动时,8t=63t,
解得,t=1,不合题意,
当点N沿C→B路径运动时,8t=3t6,
解得,t=3.5,
当点N沿B→C路径运动时,8t=3t12,
解得,t=5,
当点N沿C→F路径运动时,8t=3t18,
解得,t=6.5,
综上所述,当t=3.5秒或5秒或6.5秒时,△MDC≌△CEN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
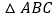 中,
中,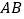 、
、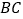 的垂直平分线相交于三角形内一点
的垂直平分线相交于三角形内一点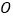 ,下列结论中,错误的是( )
,下列结论中,错误的是( )A. 点
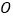 在
在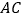 的垂直平分线上
的垂直平分线上B.
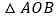 、
、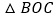 、
、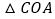 都是等腰三角形
都是等腰三角形C.
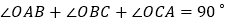
D. 点
 到
到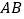 、
、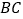 、
、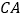 的距离相等
的距离相等 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
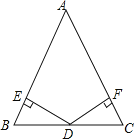
(1)求证:DE=DF;
(2)若∠A=60°,BE=1,求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,长方形的两边长分别为m+3,m+13;如图2的长方形的两边长分别为m+5,m+7.(其中m为正整数)
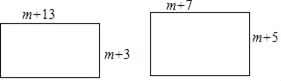
(1)写出两个长方形的面积S1,S2,并比较S1,S2的大小;
(2)现有一个正方形的周长与图1中的长方形的周长相等.试探究该正方形的面积与长方形的面积的差是否是一个常数,如果是,求出这个常数;如果不是,说明理由.
(3)在(1)的条件下,若某个图形的面积介于S1,S2之间(不包括S1,S2)且面积为整数,这样的整数值有且只有19个,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知
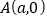 ,
,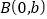 分别为两坐标轴上的点,且
分别为两坐标轴上的点,且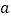 ,
,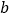 满足
满足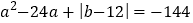 ,且
,且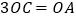 .
.(1)求
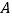 、
、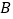 、
、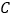 三点的坐标;
三点的坐标;(2)若
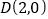 ,过点
,过点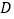 的直线分别交
的直线分别交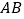 、
、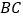 于
于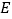 、
、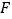 两点,且
两点,且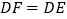 ,设
,设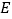 、
、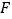 两点的横坐标分别为
两点的横坐标分别为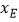 、
、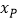 ,求
,求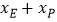 的值;
的值;(3)如图2,若
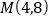 ,点
,点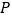 是
是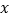 轴上
轴上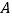 点右侧一动点,
点右侧一动点,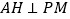 于点
于点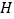 ,在
,在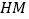 上取点
上取点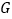 ,使
,使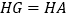 ,连接
,连接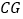 ,当点
,当点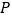 在点
在点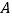 右侧运动时,
右侧运动时,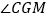 的度数是否改变?若不变,请求其值;若改变,请说明理由.
的度数是否改变?若不变,请求其值;若改变,请说明理由.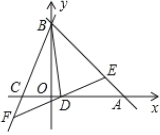
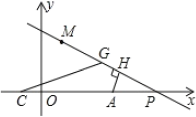
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则结论:①PA平分∠RPS;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=﹣
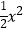 +bx+c的图象经过A(2,0)、B(0,﹣6)两点.
+bx+c的图象经过A(2,0)、B(0,﹣6)两点.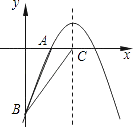
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.
相关试题

