【题目】如图1,已知![]() ,
,![]() 分别为两坐标轴上的点,且
分别为两坐标轴上的点,且![]() ,
,![]() 满足
满足![]() ,且
,且![]() .
.
(1)求![]() 、
、![]() 、
、![]() 三点的坐标;
三点的坐标;
(2)若![]() ,过点
,过点![]() 的直线分别交
的直线分别交![]() 、
、![]() 于
于![]() 、
、![]() 两点,且
两点,且![]() ,设
,设![]() 、
、![]() 两点的横坐标分别为
两点的横坐标分别为![]() 、
、![]() ,求
,求![]() 的值;
的值;
(3)如图2,若![]() ,点
,点![]() 是
是![]() 轴上
轴上![]() 点右侧一动点,
点右侧一动点,![]() 于点
于点![]() ,在
,在![]() 上取点
上取点![]() ,使
,使![]() ,连接
,连接![]() ,当点
,当点![]() 在点
在点![]() 右侧运动时,
右侧运动时,![]() 的度数是否改变?若不变,请求其值;若改变,请说明理由.
的度数是否改变?若不变,请求其值;若改变,请说明理由.
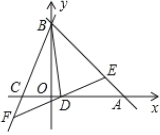
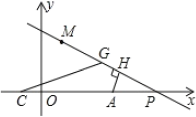
图1 图2
参考答案:
【答案】(1) A(12,0),B(0,12),C(4,0);
(2)![]()
(3) 不改变,![]()
【解析】
(1)由偶次方和绝对值的非负性质求出a和b的值,得出点A、B的坐标,再求出OC,即可得出点C的坐标;
(2)作EG⊥x轴于G,FH⊥x轴于H,DF=DE,由AAS证明△FDH≌△EDG,得出DH=DG,即可得出结果;
(3)连接MA、MC,过C作CT⊥PM于T,证明△CMT≌△MAH,可证明△CGT是等腰直角三角形,可求得∠CGM=45°.
(1)∵![]() ,
,
![]()
∴a12=0,b12=0,
∴a=b=12,
∴A(12,0),B(0,12),
∴OA=OB=12,
∵![]() .
.
∴OC=4,
∴C(4,0);
(2)作EG⊥x轴于G,FH⊥x轴于H,如图1所示:
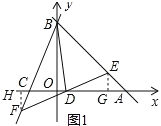
则![]()
在△FDH和△EDG中,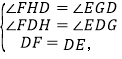
∴△FDH≌△EDG(AAS),
∴DH=DG,即![]()
∴![]()
(3)∠CGM的度数不改变,![]()
如图3,连接MA、MC,过C作CT⊥PM于T,过M作MS⊥x轴于点S,
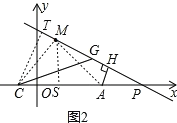
∵M(4,8),C(4,0),A(12,0),
∴S(4,0),
∴MS垂直平分AC,
∴MC=MA,且MS=SC,
∴![]()
∴![]()
∴∠TCM=∠AMH,
在△CMT和△MAH中
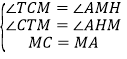
∴△CMT≌△MAH(AAS),
∴TM=AH,CT=MH,
又AH=HG
∴MT=GH,
∴GT=GM+MT=MG+GH=MH=CT,
∴△CGT是等腰直角三角形,
∴![]()
即当点P在点A右侧运动时,∠CGM的度数不改变.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
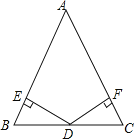
(1)求证:DE=DF;
(2)若∠A=60°,BE=1,求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,长方形的两边长分别为m+3,m+13;如图2的长方形的两边长分别为m+5,m+7.(其中m为正整数)
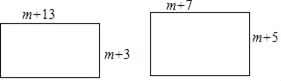
(1)写出两个长方形的面积S1,S2,并比较S1,S2的大小;
(2)现有一个正方形的周长与图1中的长方形的周长相等.试探究该正方形的面积与长方形的面积的差是否是一个常数,如果是,求出这个常数;如果不是,说明理由.
(3)在(1)的条件下,若某个图形的面积介于S1,S2之间(不包括S1,S2)且面积为整数,这样的整数值有且只有19个,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直角三角形
 中,
中,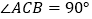 ,直线
,直线 过点
过点 .
.(1)当
 时,如图1,分别过点
时,如图1,分别过点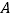 和
和 作
作 直线
直线 于点
于点 ,
, 直线
直线 于点
于点 .
. 与
与 是否全等,并说明理由;
是否全等,并说明理由;(2)当
 ,
,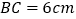 时,如图2,点
时,如图2,点 与点
与点 关于直线
关于直线 对称,连接
对称,连接 、
、 .点
.点 是
是 上一点,点
上一点,点 是
是 上一点,分别过点
上一点,分别过点 、
、 作
作 直线
直线 于点
于点 ,
, 直线
直线 于点
于点 ,点
,点 从
从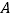 点出发,以每秒
点出发,以每秒 的速度沿
的速度沿 路径运动,终点为
路径运动,终点为 .点
.点 从点
从点 出发,以每秒
出发,以每秒 的速度沿
的速度沿 路径运动,终点为
路径运动,终点为 .点
.点 、
、 同时开始运动,各自达到相应的终点时停止运动,设运动时间为
同时开始运动,各自达到相应的终点时停止运动,设运动时间为 秒.
秒.①当
 为等腰直角三角形时,求
为等腰直角三角形时,求 的值;
的值;②当
 与
与 全等时,求
全等时,求 的值.
的值.

图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则结论:①PA平分∠RPS;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=﹣
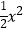 +bx+c的图象经过A(2,0)、B(0,﹣6)两点.
+bx+c的图象经过A(2,0)、B(0,﹣6)两点.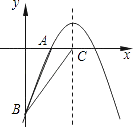
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(
 ,
,  )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由.
相关试题

