【题目】如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则结论:①PA平分∠RPS;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
参考答案:
【答案】B
【解析】根据已知条件利用HL易证△APR≌△APS,再利用全等三角形的性质可得∠PAR=∠PAS,AR=AS,从而可证(1)、(2)正确;由AQ=PQ,利用等边对等角易得∠1=∠APQ,再利用三角形外角的性质可得∠PQC=2∠1,而(1)中PA是∠BAC的角平分线可得∠BAC=2∠1,等量代换,从而有∠PQC=∠BAC,利用同位角相等两直线平行可得QP∥AR,(3)正确;根据已知条件可知△BRP与△CSP只有一角、一边对应相等,故不能证明两三角形全等,因此(4)不正确.
解:(1)PA平分∠BAC.∵PR⊥AB,PS⊥AC,PR=PS,AP=AP,∴△APR≌△APS,∴∠PAR=∠PAS,∴PA平分∠BAC;
(2)由(1)中的全等也可得AS=AR;
(3)如图所示
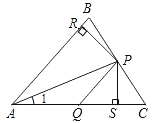
∵AQ=PR,∴∠1=∠APQ,∴∠PQS=∠1+∠APQ=2∠1,又∵PA平分∠BAC,∴∠BAC=2∠1,∴∠PQS=∠BAC,∴PQ∥AR;
(4)∵PR⊥AB,PS⊥AC,∴∠BRP=∠CSP,∵PR=PS,∴△BRP不一定全等与△CSP(只具备一角一边的两三角形不一定全等).故选B.
“点睛“本题考查了全等三角形的判定和性质;做题时利用了平行线的判定、等边对等角、三角形外角的性质,要熟练掌握这些知识并能灵活应用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出命题“内错角相等”的逆命题_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据由五个正整数组成,中位数是3,且惟一众数是7,则这五个正整数的平均数是( )
A.4B.5C.6D.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简
(1)6ab﹣20a3﹣4ba+19a3
(2)3(3x+2y)﹣2(2x﹣3y)
-
科目: 来源: 题型:
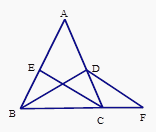
查看答案和解析>>【题目】如图所示,∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F,问CE与DF的位置关系?试说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列小题
(1)如图①,若∠B+∠D=∠BED,试猜想AB与CD的位置关系,并说明理由。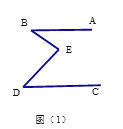
(2)如图②,要想得到AB∥CD,则∠1、∠2、∠3之间应满足怎样的位置关系?请探索。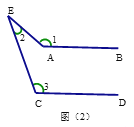
-
科目: 来源: 题型:
查看答案和解析>>【题目】现规定一种新运算△,满足x△y=x2﹣y,例如3△2=32﹣2=7.
(1)求4△(﹣3)的值;
(2)求(﹣1△2)△(﹣2)的值.
相关试题

