【题目】已知如图:△ABC中,∠B、∠C的平分线相交于点O,过点O作EF∥BC交AB、AC于E、F.
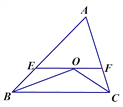
(1)图中有几个等腰三角形?试说明理由,并请指出EF与BE、CF间有怎样的关系?
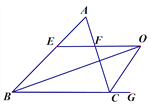
(2)若△ABC中,∠B的平分线与三角形外角∠ACG的平分线CO交于点O,过O点作OE∥BC交AB于E,交AC于F(如图2),请直接写出EF与BE、CF间的关系,不用证明.
参考答案:
【答案】(1)有2个等腰三角形分别是:等腰△OBE和等腰△OCF;(2)EF=BE-CF
【解析】试题分析:(1)根据角平分线的定义可得: ∠EBO=∠CBO,∠FCO=∠BCO,根据两直线平行内错角相等的性质可得:∠EOB=∠CBO,∠FOC=∠BCO,等量代换可得:∠EBO=∠EOB,∠FCO=∠FOC,利用等角对等边可判定:BE=EO,FO=CF,所以△OBE和△OCF是等腰三角形,又因为EF=OE+OF,所以EF=BE+CF,
(2) 根据角平分线的定义可得: ∠EBO=∠CBO,∠FCO=∠OCG,根据两直线平行内错角相等的性质可得:∠EOB=∠CBO,∠FOC=∠OCG,等量代换可得:∠EBO=∠EOB,∠FCO=∠FOC,利用等角对等边可判定:BE=EO,FO=CF,所以△OBE和△OCF是等腰三角形,又因为EF=OE-OF,所以EF=BE-CF.
试题解析:(1)有2个等腰三角形分别是:等腰△OBE和等腰△OCF,
理由如下:OB平分∠ABC,
∴∠ABO=∠OBC,
∵EF∥BC,
∴∠EOB=∠OBC,
∴∠ABO=∠EOB,
∴EO=EB,
∴△OBE是等腰三角形,
同理FO=FC,△OCF是等腰三角形,
∴EF=OE+OF=BE+CF,
(2)EF=BE-CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=2是关于x的方程2(x-m)=8x-4m的解,求m的值.
-
科目: 来源: 题型:
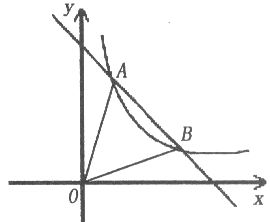
查看答案和解析>>【题目】如图,一次函数y=k1x+b的图象与反比例函数y=
 的图象交于A(1,4),B(3,m)两点。
的图象交于A(1,4),B(3,m)两点。(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】2x+10>2的解集是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知今年甲的年龄比乙的年龄多12岁,4年后甲的年龄恰好是乙的年龄的2倍,则甲今年的年龄是( )
A. 20岁 B. 16岁 C. 15岁 D. 12岁
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,9,7,26,17,9.这组数据的众数是( )
A.17B.7C.16D.15
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式计算正确的是( )
A.6a+2a=8a2
B.(a﹣b)2=a2﹣b2
C.a4a6=a10
D.(a3)2=a5
相关试题

