【题目】如图,长方形纸片ABCD中,AB=8cm,AD=6cm,按下列步骤进行裁剪和拼图: 
第一步:如图①,在线段AD上任意取一点E,沿EB,EC剪下一个三角形纸片EBC(余下部分不再使用);
第二步:如图②,沿三角形EBC的中位线GH将纸片剪成两部分,并在线段GH上任意取一点M,线段BC上任意取一点N,沿MN将梯形纸片GBCH剪成两部分;
第三步:如图③,将MN左侧纸片绕G点按顺时针方向旋转180°,使线段GB与GE重合,将MN右侧纸片绕H点按逆时针方向旋转180°,使线段HC与HE重合,拼成一个与三角形纸片EBC面积相等的四边形纸片.
(注:裁剪和拼图过程均无缝且不重叠)
则拼成的这个四边形纸片的周长的最小值为cm,最大值为cm.
参考答案:
【答案】20;12+ ![]()
【解析】解:画出第三步剪拼之后的四边形M1N1N2M2的示意图,如答图1所示. 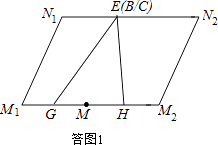
图中,N1N2=EN1+EN2=NB+NC=BC,
M1M2=M1G+GM+MH+M2H=2(GM+MH)=2GH=BC(三角形中位线定理),
又∵M1M2∥N1N2 , ∴四边形M1N1N2M2是一个平行四边形,
其周长为2N1N2+2M1N1=2BC+2MN.
∵BC=6为定值,∴四边形的周长取决于MN的大小.
如答图2所示,是剪拼之前的完整示意图.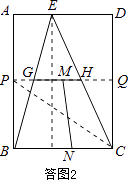
过G、H点作BC边的平行线,分别交AB、CD于P点、Q点,则四边形PBCQ是一个矩形,这个矩形是矩形ABCD的一半.
∵M是线段GH上的任意一点,N是线段BC上的任意一点,
根据垂线段最短,得到MN的最小值为PQ与BC平行线之间的距离,即MN最小值为4;
而MN的最大值等于矩形对角线的长度,即 ![]() =
= ![]() =
= ![]()
∵四边形M1N1N2M2的周长=2BC+2MN=12+2MN,
∴四边形M1N1N2M2周长的最小值为12+2×4=20,
最大值为12+2× ![]() =12+
=12+ ![]() .
.
所以答案是:20,12+ ![]() .
.
【考点精析】掌握三角形中位线定理和矩形的性质是解答本题的根本,需要知道连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;矩形的四个角都是直角,矩形的对角线相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们给出如下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形.请解答下列问题:
(1)写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称;
(2)探究:当等对角线四边形中两条对角线所夹锐角为60°时,这对60°角所对的两边之和与其中一条对角线的大小关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.
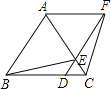
(1)请在图中找出一对全等三角形,用符号“≌”表示,并加以证明;
(2)判断四边形ABDF是怎样的四边形,并说明理由;
(3)若AB=6,BD=2DC,求四边形ABEF的面积..
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB。

(1)用尺规作图的方法作出线段AB的垂直平分线l(保留作图痕迹,不要求写出作法);
(2)在(1)中所作的直线l上任意取两点M、N(线段AB的上方),连接AM、AN。BM、BN。
求证:∠MAN=∠MBN。
-
科目: 来源: 题型:
查看答案和解析>>【题目】9岁的小芳身高1.36米,她的表姐明年想报考北京的大学.表姐的父母打算今年暑假带着小芳及其表姐先去北京旅游一趟,对北京有所了解.他们四人7月31日下午从苏州出发,1日到4日在北京旅游,8月5日上午返回苏州.
苏州与北京之间的火车票和飞机票价如下:火车 (高铁二等座) 全票524元,身高1.1~1.5米的儿童享受半价票;飞机 (普通舱) 全票1240元,已满2周岁未满12周岁的儿童享受半价票.他们往北京的开支预计如下:
住宿费
(2人一间的标准间)
伙食费
市内交通费
旅游景点门票费
(身高超过1.2米全票)
每间每天x元
每人每天100元
每人每天y元
每人每天120元
假设他们四人在北京的住宿费刚好等于上表所示其他三项费用之和,7月31日和8月5日合计按一天计算,不参观景点,但产生住宿、伙食、市内交通三项费用.
(1)他们往返都坐火车,结算下来本次旅游总共开支了13668元,求x,y的值;
(2)他们往返都坐飞机 (成人票五五折),其他开支不变,至少要准备多少元?
(3)他们去时坐火车,回来坐飞机 (成人票五五折),其他开支不变,准备了14000元,是否够用?如果不够,他们准备不再增加开支,而是压缩住宿的费用,请问他们预定的标准间房价每天不能超过多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,点D、E分别在边AC、BC上(不与点A、B、C重合),点P是直线AB上的任意一点(不与点A、B重合).设∠PDA=x,∠PEB=y,∠DPE=m,∠C=n.
(1)如图,当点P在线段AB上运动,且n=90°时
①若PD∥BC,PE∥AC,则m=_____;
②若m=50°,求x+y的值.
(2)当点P在直线AB上运动时,直接写出x、y、m、n之间的数量关系.


-
科目: 来源: 题型:
查看答案和解析>>【题目】某班45名学生的成绩被分为5组,第1~4组的频数分别为12,11,9,4,则第5组的频率是( )
A.0.1B.0.2C.0.3D.0.4
相关试题

