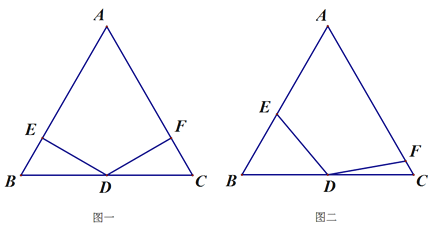
【题目】在等边△ABC中,点D是线段BC的中点,∠EDF=120°,线段DE与线段AB相交于点E.线段DF与线段AC相交于点F.
(1)如图一,若DF⊥AC,请直接写出DE与AB的位置关系;
(2)请判断DE与DF的数量关系.并写出推理过程.
(3)如图二,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F. (2)中的结论还成立吗?若成立,写出证明过程,若不成立,说明理由.
(4)在∠EDF绕点D顺时针旋转过程中,直接用等式表示线段BE、CF、AB之间的数量关系。
参考答案:
【答案】(1)DE⊥AB;(2)DE=DF 证明见解析;(3)成立.证明见解析;(4)BE+CF=![]()
【解析】试题分析:(1)DE⊥AB,根据四边形的内角和定理即可求得∠AED=90°,所以DE⊥AB;(2)方法①可以通过AAS证明△BED≌△CFD,得出结论;方法 ②也可以连接AD通过等腰三角形三线合一得出AD平分∠BAC,利用角平分线性质定理得出;(3)成立,证明:方法①可以恢复到图一,在图一的基础上证明全等得出结论;方法②也可以取AB中点M,连接DM证明△EDM≌△FDC即可;(4)取AB中点M,连接DM证明△EDM≌△FDC即可得结论.
试题解析:
(1)DE⊥AB
(2)DE=DF 证明:①可以通过AAS证明△BED≌△CFD,得出结论
②也可以连接AD通过等腰三角形三线合一得出AD平分∠BAC,利用角平分线性质定理得出.
成立.证明①可以恢复到图一,在图一的基础上证明全等得出结论.
②也可以取AB中点M,连接DM证明△EDM≌△FDC即可.
(4)BE+CF=![]()
-
科目: 来源: 题型:
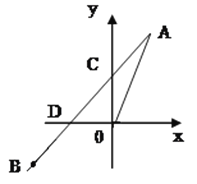
查看答案和解析>>【题目】如图正比例函数y=2x的图像与一次函数 y=kx+b的图像交于点A(m,2),一次函数的图像经过点B(-2,-1)与y轴交点为C,与x轴交点为D.
(1)求m的值;
(2)求一次函数的解析式;
(3)求C点的坐标;
(4)求△AOD的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:
(1)6ab2﹣8a2b3
(2)(a﹣b)+c2(b﹣a)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知函数y=-x+b的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=-x+b和y=x的图象于点C,D.
(1)求点A的坐标;(2)若OB=CD,求a的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线的顶点为(4,﹣8),并且经过点(6,﹣4),试确定此抛物线的解析式.并写出对称轴方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线与x轴交于A,B两点,与y轴交于C点,点A的坐标为(2,0),点C的坐标为(0,3),它的对称轴是直线x=-
 .
.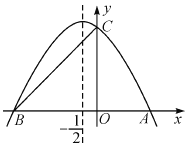
(1)求抛物线的解析式;
(2)M是线段AB上的任意一点,当△MBC为等腰三角形时,求M点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
相关试题

