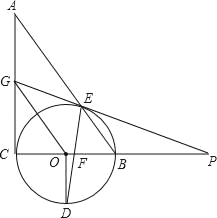
【题目】如图,Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于E,OD⊥BC交⊙O于D,DE交BC于F,点P为CB延长线上的一点,PE延长交AC于G,PE=PF,下列4个结论:①GE=GC;②AG=GE;③OG∥BE;④∠A=∠P.其中正确的结论是_____(填写所有正确结论的序号)
参考答案:
【答案】①②③
【解析】连接OE,CE,
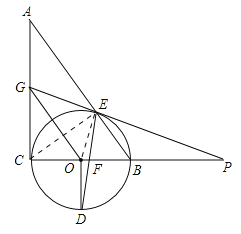
∵OE=OD,PE=PF,
∴∠OED=∠ODE,∠PEF=∠PFE,
∵OD⊥BC,
∴∠ODE+∠OFD=90°,
∵∠OFD=∠PFE,
∴∠OED+∠PEF=90°,
即OE⊥PE,
∵点E⊙O上,
∴PE为⊙O的切线;故①正确;
∵BC是直径,
∴∠BEC=90°,
∴∠AEC=90°
∵∠ACB=90°,
∴AC是⊙O的切线,
∴EG=CG,
∴∠GCE=∠GEC,
∵∠GCE+∠A=90°,∠GEC+∠AEG=90°,
∴∠A=∠AEG,
∴AG=EG,
∴AG=CG,
即G为AC的中点;故②正确;
∵OC=OB,
∴OG是△ABC的中位线,
∴OG∥AB,
即OG∥BE,故③正确;
在Rt△ABC中,∠A+∠ABC=90°,
在Rt△POE中,∠P+∠POE=90°,
∵OE=OB,
∴∠OBE=∠OEB,
但∠POE不一定等于∠ABC,
∴∠A不一定等于∠P.故④错误.
故答案为①②③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC. 已知AB=2,DE=1,BD=8,设CD=x.
(1)用含x的代数式表示AC+CE的长;
(2)求AC+CE的值最小;
(3)根据(2)中的规律和结论,请构图求出代数式
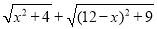 的最小值。
的最小值。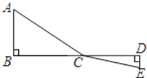
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解题:
学习了二次根式后,你会发现一些含有根号的式子可以写成另一个式子的平方,如
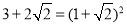 ,我们来进行以下的探索:
,我们来进行以下的探索:设
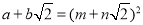 (其中a,b,m,n都是正整数),则有
(其中a,b,m,n都是正整数),则有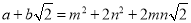 ,∴
,∴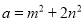 ,
,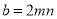 ,这样就得出了把类似
,这样就得出了把类似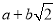 的式子化为平方式的方法.
的式子化为平方式的方法.请仿照上述方法探索并解决下列问题:
(1)当a,b,m,n都是正整数时,若
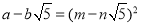 ,用含m,n的式子分别表示a,b,得a= ,b= ;
,用含m,n的式子分别表示a,b,得a= ,b= ;(2)利用上述方法,找一组正整数a,b,m,n,填空:
﹣
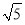 =( —
=( — 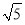 )2
)2(3)
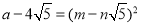 且a,m,n都为正整数,求a的值.
且a,m,n都为正整数,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离是 ;表示-3和2两点之间的距离是 ;一般地,数轴上表示数m和数n的两点之间的距离等于|m-n|.
(2)如果|x+1|=3,那么x= ;
(3)若|a-3|=2,|b+2|=1,且数a、b在数轴上表示的数分别是点A、点B,则A、B 两点间的最大距离是 .
(4)若数轴上表示a的点位于-4与2之间,则|a+4|+|a-2= .
-
科目: 来源: 题型:
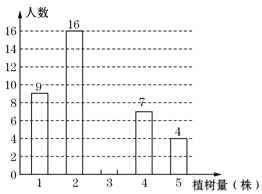
查看答案和解析>>【题目】为了发展乡村旅游,建设美丽从化,某中学七年级一班同学都积极参加了植树活动,今年四月份该班同学的植树情况部分如图所示,且植树2株的人数占32%.
(1)求该班的总人数、植树株数的众数,并把条形统计图补充完整;
(2)若将该班同学的植树人数所占比例绘制成扇形统计图时,求“植树3株”对应扇形的圆心角的度数;
(3)求从该班参加植树的学生中任意抽取一名,其植树株数超过该班植树株数的平均数的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为举办校园文化艺术节,甲、乙两班准备给合唱同学购买演出服装(一人一套),两班共92人(其中甲班比乙班人多,且甲班不到90人),下面是供货商给出的演出服装的价格表:
购买服装的套数
1套至45套
46套至90套
91套以上
每套服装的价格
60元
50元
40元
如果两班单独给每位同学购买一套服装,那么一共应付5020元.
(1)甲、乙两班联合起来给每位同学购买一套服装,比单独购买可以节省多少钱?
(2)甲、乙两班各有多少名同学?
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入相应的集合内:+8.5,-3
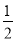 ,0.3,0,-3.4,12,-9,4
,0.3,0,-3.4,12,-9,4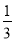 ,-1.2,-2.
,-1.2,-2.(1)正数集合:{___________…};
(2)整数集合:{___________…};
(3)非正整数集合:{_____________…};
(4)负分数集合:{ ________________…}.
相关试题

