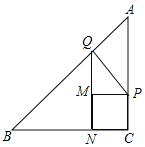
【题目】如图,在Rt![]() ABC中,∠C=90°,AC=BC=4cm,动点P从点C出发以1cm/s的速度沿CA匀速运动,同时动点Q从点A出发以
ABC中,∠C=90°,AC=BC=4cm,动点P从点C出发以1cm/s的速度沿CA匀速运动,同时动点Q从点A出发以![]() 的速度沿AB匀速运动,当点P到达点A时,点P、Q同时停止运动,设运动时间为他t(s).
的速度沿AB匀速运动,当点P到达点A时,点P、Q同时停止运动,设运动时间为他t(s).
(1)当t为何值时,点B在线段PQ的垂直平分线上?
(2)是否存在某一时刻t,使![]() APQ是以PQ为腰的等腰三角形?若存在,求出
APQ是以PQ为腰的等腰三角形?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)以PC为边,往CB方向作正方形CPMN,设四边形QNCP的面积为S,求S关于t的函数关系式.
参考答案:
【答案】(1)![]() (2)存在,
(2)存在,![]() 或2
或2![]() (3)
(3)![]()
【解析】
(1)连接PB,由点B在线段PQ的垂直平分线上,推出BP=BQ,由此构建方程即可解决问题;(2)分两种情形分别构建方程求解即可;(3)如图4中,连接QC,作QE⊥AC于E,作QF⊥BC于F.则QE=AE,![]() ,可得QE+QF=AE+EC=AC=4.根据S=
,可得QE+QF=AE+EC=AC=4.根据S=![]() ,计算即可;
,计算即可;
(1)如图1中,连接![]() .
.

在![]() 中,
中,![]() ,
,![]() ,
,![]()
![]() 点
点![]() 在线段
在线段![]() 的垂直平分线上,
的垂直平分线上,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
解得![]() 或
或![]() (舍弃),
(舍弃),
![]() 时,点
时,点![]() 在线段
在线段![]() 的垂直平分线上.
的垂直平分线上.
(2)①如图2中,当![]() 时,易知
时,易知![]() 是等腰直角三角形,
是等腰直角三角形,![]() .
.
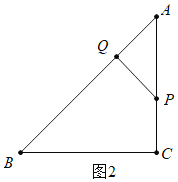
则有![]() ,
,
![]() ,
,
解得![]() .
.
②如图3中,当![]() 时,易知
时,易知![]() 是等腰直角三角形,
是等腰直角三角形,![]() .
.
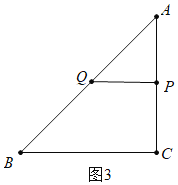
则有:![]() ,
,
![]()
![]() ,
,
解得![]() ,
,
综上所述:![]() 或
或![]() 时,
时,![]() 是以
是以![]() 为腰的等腰三角形.
为腰的等腰三角形.
(3)如图4中,连接![]() ,作
,作![]() 于
于![]() ,作
,作![]() 于
于![]() .则
.则![]() ,
,![]() ,可得
,可得![]() .
.
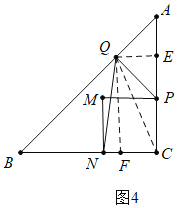
![]() .
.
-
科目: 来源: 题型:
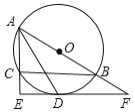
查看答案和解析>>【题目】如图,
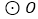 是
是 ABC的外接圆,AB为直径,∠BAC的平分线交
ABC的外接圆,AB为直径,∠BAC的平分线交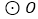 于点D,过点D作DE
于点D,过点D作DE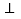 AC分别交AC、AB的延长线于点E、F.
AC分别交AC、AB的延长线于点E、F.(1)求证:EF是
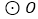 的切线;
的切线;(2)若AC=4,CE=2,求
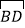 的长度.(结果保留
的长度.(结果保留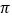 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量
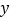 (件
(件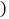 与销售价
与销售价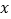 (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.(1)求
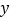 与
与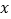 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量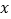 的取值范围;
的取值范围;(2)求每天的销售利润W(元
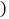 与销售价
与销售价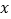 (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
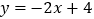 分别交
分别交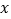 轴、
轴、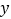 轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC
轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC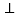
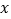 轴于点C,交抛物线于点D.
轴于点C,交抛物线于点D.(1)若抛物线的解析式为
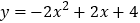 ,设其顶点为M,其对称轴交AB于点N.
,设其顶点为M,其对称轴交AB于点N.①求点M、N的坐标;
②是否存在点P,使四边形MNPD为菱形?并说明理由;
(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与
 AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.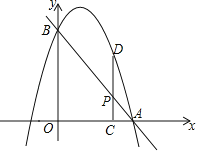
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数 y=ax2+bx+c(a≠0)的图象如图,有下列 5 个结论:①4a+2b+c>0;②abc<0;③b<a+c;④3b>2c;⑤a+b<m(am+b),(m≠1 的实数);其中正确结论的个数为( )
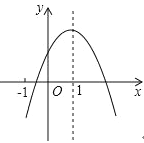
A. 2 个 B. 3 个 C. 4 个 D. 5 个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,直径AB垂直弦CD,E为BC弧上一点,下列结论:①∠1=∠2;②∠3=2∠4;③∠3+∠5=180°,其中正确的是( )
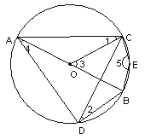
A. ①③ B. ②③
C. ①②③ D. ①②
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的方程x2-2(m+1)x+m2=0.
(1)当m取何值时,方程有两个实数根?
(2)为m选取一个合适的整数,使方程有两个不相等的实数根,并求这两个根.
相关试题

