【题目】如图,已知直线![]() 分别交
分别交![]() 轴、
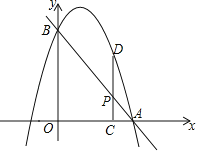
轴、![]() 轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC
轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC![]()
![]() 轴于点C,交抛物线于点D.
轴于点C,交抛物线于点D.
(1)若抛物线的解析式为![]() ,设其顶点为M,其对称轴交AB于点N.
,设其顶点为M,其对称轴交AB于点N.
①求点M、N的坐标;
②是否存在点P,使四边形MNPD为菱形?并说明理由;
(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与![]() AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
参考答案:
【答案】(1)①![]()
![]() ②答案见解析 (2)存在,
②答案见解析 (2)存在,![]() 或
或![]()
【解析】
(1)①如图1,把抛物线解析式配成顶点式可得到顶点为![]() 的坐标为
的坐标为![]() ,
,![]() ,然后计算自变量为
,然后计算自变量为![]() 对应的一次函数值可得到
对应的一次函数值可得到![]() 点坐标;
点坐标;
②易得![]() ,设
,设![]() 点坐标为
点坐标为![]() ,则
,则![]() ,则
,则![]() ,由于
,由于![]() ,根据平行四边形的判定方法,当
,根据平行四边形的判定方法,当![]() 时,四边形
时,四边形![]() 为平行四边形,即
为平行四边形,即![]() ,求出
,求出![]() 得到此时
得到此时![]() 点坐标为
点坐标为![]() ,
,![]() ,接着计算出
,接着计算出![]() ,然后比较
,然后比较![]() 与
与![]() 的大小关系可判断平行四边形
的大小关系可判断平行四边形![]() 是否为菱形;
是否为菱形;
(2)如图2,利用勾股定理计算出![]() ,再表示出
,再表示出![]() ,则可计算出
,则可计算出![]() ,接着表示出抛物线解析式为
,接着表示出抛物线解析式为![]() ,则可用
,则可用![]() 表示出点
表示出点![]() 坐标为
坐标为![]() ,所以
,所以![]() ,由于
,由于![]() ,根据相似三角形的判定方法,当
,根据相似三角形的判定方法,当![]() 时,
时,![]() ,即
,即![]() ;当
;当![]() 时,
时,![]() ,即
,即![]() ,然后利用比例性质分别求出
,然后利用比例性质分别求出![]() 的值,从而得到对应的抛物线的解析式.
的值,从而得到对应的抛物线的解析式.
(1)①如图1,
![]() ,
,
![]() 顶点为
顶点为![]() 的坐标为
的坐标为![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,则点
,则点![]() 坐标为
坐标为![]() ,
,![]() ;
;
②不存在.
理由如下:
![]() ,
,
设![]() 点坐标为
点坐标为![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,四边形
时,四边形![]() 为平行四边形,即
为平行四边形,即![]() ,解得
,解得![]() (舍去),
(舍去),![]() ,此时
,此时![]() 点坐标为
点坐标为![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 平行四边形
平行四边形![]() 不为菱形,
不为菱形,
![]() 不存在点
不存在点![]() ,使四边形
,使四边形![]() 为菱形;
为菱形;
(2)存在.
如图2,![]() ,
,![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,
,
![]() ,
,
设抛物线的解析式为![]() ,
,
把![]() 代入得
代入得![]() ,解得
,解得![]() ,
,
![]() 抛物线的解析式为
抛物线的解析式为![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 当
当![]() 时,
时,![]() ,即
,即![]() ,解得
,解得![]() ,此时抛物线解析式为
,此时抛物线解析式为![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ,解得
,解得![]() ,此时抛物线解析式为
,此时抛物线解析式为![]() ;
;
综上所述,满足条件的抛物线的解析式为![]() 或
或![]() .
.
-
科目: 来源: 题型:
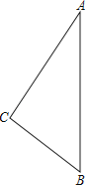
查看答案和解析>>【题目】一名徒步爱好者来衡阳旅行,他从宾馆C出发,沿北偏东30°的方向行走2000米到达石鼓书院A处,参观后又从A处沿正南方向行走一段距离,到达位于宾馆南偏东45°方向的雁峰公园B处,如图所示.
(1)求这名徒步爱好者从石鼓书院走到雁峰公园的途中与宾馆之间的最短距离;
(2)若这名徒步爱好者以100米/分的速度从雁峰公园返回宾馆,那么他在15分钟内能否到达宾馆?
-
科目: 来源: 题型:
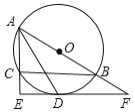
查看答案和解析>>【题目】如图,
 是
是 ABC的外接圆,AB为直径,∠BAC的平分线交
ABC的外接圆,AB为直径,∠BAC的平分线交 于点D,过点D作DE
于点D,过点D作DE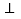 AC分别交AC、AB的延长线于点E、F.
AC分别交AC、AB的延长线于点E、F.(1)求证:EF是
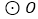 的切线;
的切线;(2)若AC=4,CE=2,求
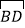 的长度.(结果保留
的长度.(结果保留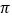 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量
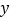 (件
(件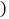 与销售价
与销售价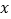 (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.(1)求
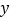 与
与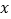 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量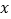 的取值范围;
的取值范围;(2)求每天的销售利润W(元
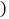 与销售价
与销售价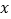 (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
-
科目: 来源: 题型:
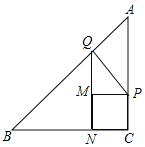
查看答案和解析>>【题目】如图,在Rt
 ABC中,∠C=90°,AC=BC=4cm,动点P从点C出发以1cm/s的速度沿CA匀速运动,同时动点Q从点A出发以
ABC中,∠C=90°,AC=BC=4cm,动点P从点C出发以1cm/s的速度沿CA匀速运动,同时动点Q从点A出发以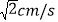 的速度沿AB匀速运动,当点P到达点A时,点P、Q同时停止运动,设运动时间为他t(s).
的速度沿AB匀速运动,当点P到达点A时,点P、Q同时停止运动,设运动时间为他t(s).(1)当t为何值时,点B在线段PQ的垂直平分线上?
(2)是否存在某一时刻t,使
 APQ是以PQ为腰的等腰三角形?若存在,求出
APQ是以PQ为腰的等腰三角形?若存在,求出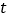 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;(3)以PC为边,往CB方向作正方形CPMN,设四边形QNCP的面积为S,求S关于t的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数 y=ax2+bx+c(a≠0)的图象如图,有下列 5 个结论:①4a+2b+c>0;②abc<0;③b<a+c;④3b>2c;⑤a+b<m(am+b),(m≠1 的实数);其中正确结论的个数为( )
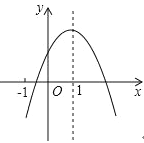
A. 2 个 B. 3 个 C. 4 个 D. 5 个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,直径AB垂直弦CD,E为BC弧上一点,下列结论:①∠1=∠2;②∠3=2∠4;③∠3+∠5=180°,其中正确的是( )
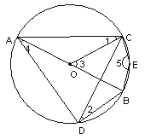
A. ①③ B. ②③
C. ①②③ D. ①②
相关试题

