【题目】如图所示,太阳光线AC和AC是平行的,同一时刻两个建筑物在太阳下的影子一样长,那么建筑物是否一样高?请说明理由.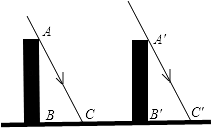
参考答案:
【答案】解:建筑物一样高.
证明:∵AB⊥BC,A′B′⊥B′C′,
∴∠ABC=∠A′B′C′=90°,
∵AC∥A′C′,
∴∠ACB=∠A′C′B′,
在△ABC和△A′B′C′中,![]()
![]()
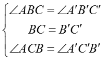 ,
,
∴△ABC≌△A′B′C′(ASA)
∴AB=A′B′.
即建筑物一样高.
【解析】根据已知同一时刻两个建筑物在太阳下的影子一样长,即可得出BC=B′C′,在直角三角形中,可考虑AAS证明三角形全等,从而推出线段相等.
【考点精析】掌握平行线的性质和平行投影是解答本题的根本,需要知道两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;太阳光线可以看成是平行光线,平行光线所形成的投影称为平行投影;作物体的平行投影:由于平行投影的光线是平行的,而物体的顶端与影子的顶端确定的直线就是光线,故根据另一物体的顶端可作出其影子.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次智力测验,有20道选择题.评分标准是:对1题给5分,错1题扣2分,不答题不给分也不扣分.小明有两道题未答.至少答对几道题,总分才不会低于60分.则小明至少答对的题数是( )
A.11道 B。12题 C.13题 D.14题
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:∠AOB=
 °,过点O作OB⊥OC.请画图示意并求解.
°,过点O作OB⊥OC.请画图示意并求解.
(1)若 =30,则∠AOC=.
=30,则∠AOC=.
(2)若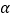 =40,射线OE平分∠AOC , 射线OF平分∠BOC , 求∠EOF的度数;
=40,射线OE平分∠AOC , 射线OF平分∠BOC , 求∠EOF的度数;
(3)若0<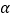 <180,射线OE平分∠AOC , 射线OF平分∠BOC , 则∠EOF=°.(用
<180,射线OE平分∠AOC , 射线OF平分∠BOC , 则∠EOF=°.(用 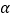 的代数式表示).
的代数式表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(x-2,3)与点B(x+4,y-5)关于原点对称,则xy的值是( )
A.2B.-2C.1D.-1
-
科目: 来源: 题型:
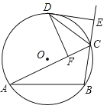
查看答案和解析>>【题目】如图,⊙O的内接△ABC的外角∠ACE的平分线交⊙O于点D.DF⊥AC,垂足为F,DE⊥BC,垂足为E.给出下列4个结论:①CE=CF;②∠ACB=∠EDF;③DE是⊙O的切线;④
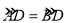 .其中一定成立的是( )
.其中一定成立的是( )A.①②③ B.②③④ C.①③④ D.①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲、乙两人均从400米的环形跑道的A处出发,各自以每秒6米和每秒8米的速度在跑道上跑步.
(1)若两人同时出发,背向而行,则经过秒钟两人第一次相遇;
若两人同时出发,同向而行,则经过秒钟乙第一次追上甲.
(2)若两人同向而行,乙在甲出发10秒钟后去追甲,经过多少时间乙第二次追上甲.
(3)若让甲先跑10秒钟后乙开始跑,在乙用时不超过100秒的情况下,乙跑多少秒钟时,两人相距40米. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )

A.
 B.
B.  C.
C.  D.
D. 
相关试题

