【题目】已知甲、乙两人均从400米的环形跑道的A处出发,各自以每秒6米和每秒8米的速度在跑道上跑步.
(1)若两人同时出发,背向而行,则经过秒钟两人第一次相遇;
若两人同时出发,同向而行,则经过秒钟乙第一次追上甲.
(2)若两人同向而行,乙在甲出发10秒钟后去追甲,经过多少时间乙第二次追上甲.
(3)若让甲先跑10秒钟后乙开始跑,在乙用时不超过100秒的情况下,乙跑多少秒钟时,两人相距40米.
参考答案:
【答案】
(1)![]()
![]() ,200
,200
(2)解:设经过x秒时乙第二次追上甲,
则8x-6x=400+6×10,
x=230(秒)
(3)解:设经过x秒时甲乙两人相距40米,
同向而行时(甲在前乙在后)60+6x-8x=40,x =10(秒);
(乙超过甲后)8x-(60+6x)=40,x=50(秒);
相向而行时(相遇前)60+6x+8x=360,x = ![]() (秒);
(秒);
(相遇后)60+6x+8x=440, x= ![]() (秒)
(秒)
【解析】解:(1)两人同时出发,背向而行,两人第一次相遇需要:400÷(8+6)=![]() (秒),
(秒),
两人同时出发,同向而行,两人第一次相遇需要:400÷(8-6)=200(秒);
(1)根据两人同时出发,背向而行,两人第一次相遇时,两人所行的路程之和为环形路程;两人同时出发,同向而行,两人第一次相遇,两人所行的路程之差为环形路程,再由时间等于路程除以速度可求出答案;
(2)设经过x秒时乙第二次追上甲,根据甲乙所行的路程之差=环形路程+甲提前跑的路程来解方程求解;
(3)设经过x秒时甲乙两人相距40米,分两人同向和背向而行来讨论求解.当同向而行时,再分甲在前乙在后和乙超过甲后列方程求解;相向而行时,分相遇前和相遇后来列方程求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(x-2,3)与点B(x+4,y-5)关于原点对称,则xy的值是( )
A.2B.-2C.1D.-1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,太阳光线AC和AC是平行的,同一时刻两个建筑物在太阳下的影子一样长,那么建筑物是否一样高?请说明理由.
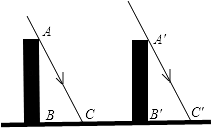
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的内接△ABC的外角∠ACE的平分线交⊙O于点D.DF⊥AC,垂足为F,DE⊥BC,垂足为E.给出下列4个结论:①CE=CF;②∠ACB=∠EDF;③DE是⊙O的切线;④
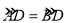 .其中一定成立的是( )
.其中一定成立的是( )A.①②③ B.②③④ C.①③④ D.①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】平移的过程中,新图形中的每一点都是由原图形中的某一点移动后得到的,这两点是______,连接各组对应点的线段________.平移后的图形的位置是由平移的_____和平移的____决定的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程(x+1)2=4的解为
A.x1=1,x2=-3B.x1=-1,x2=3C.x1=2,x2=-2D.x1=1,x2=-1
相关试题

