【题目】已知:∠AOB= ![]() °,过点O作OB⊥OC.请画图示意并求解.
°,过点O作OB⊥OC.请画图示意并求解.
(1)若 ![]() =30,则∠AOC=.
=30,则∠AOC=.
(2)若 ![]() =40,射线OE平分∠AOC , 射线OF平分∠BOC , 求∠EOF的度数;
=40,射线OE平分∠AOC , 射线OF平分∠BOC , 求∠EOF的度数;
(3)若0< ![]() <180,射线OE平分∠AOC , 射线OF平分∠BOC , 则∠EOF=°.(用
<180,射线OE平分∠AOC , 射线OF平分∠BOC , 则∠EOF=°.(用 ![]() 的代数式表示).
的代数式表示).
参考答案:
【答案】
(1)120°或60°
(2)解:示意图画出,20°;
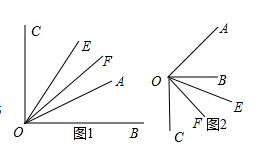
当射线OA,OC在射线OB同侧时,
∵OE平分∠AOC,OF平分∠BOC,
∴∠COE=![]() ∠AOC,∠COF=
∠AOC,∠COF=![]() ∠BOC,
∠BOC,
∴∠EOF=∠COF-∠COE=![]() (∠BOC-∠AOC)=
(∠BOC-∠AOC)=![]() (90°-90°+40°)=20°;
(90°-90°+40°)=20°;
当射线OA,OC在射线OB两侧时,
∠EOF=∠COF-∠COE=![]() (∠BOC-∠AOC)=
(∠BOC-∠AOC)=![]() (90°+40°-90°)=20°,
(90°+40°-90°)=20°,
故∠EOF为20°;
(3)![]()
![]()
【解析】解:(1)∵OB⊥OC,
∴∠BOC=90°,
当射线OA,OC在射线OB同侧时,∠AOC=∠AOB-∠BOC=60°,
当射线OA,OC在射线OB两侧时,∠AOC=∠AOB+∠BOC=120°;
所以答案是:120°或60°;
(3)当射线OA,OC在射线OB同侧时,
∵OE平分∠AOC,OF平分∠BOC,
∴∠COE=![]() ∠AOC,∠COF=
∠AOC,∠COF=![]() ∠BOC,
∠BOC,
∴∠EOF=∠COF-∠COE=![]() (∠BOC-∠AOC)=
(∠BOC-∠AOC)=![]() (90°-90°+
(90°-90°+![]() )=
)=![]() °;
°;
当射线OA,OC在射线OB两侧时,
∠EOF=∠COF-∠COE=![]() (∠BOC-∠AOC)=
(∠BOC-∠AOC)=![]() (90°+
(90°+![]() -90°)=
-90°)=![]() .
.
所以答案是:![]() .
.
(1)分射线OA,OC在射线OB同侧和两侧来讨论求解;
(2)分射线OA,OC在射线OB同侧和两侧来讨论,再由角平分线的定义来求解;
(3)与(2)解法相同.
【考点精析】解答此题的关键在于理解角的平分线的相关知识,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线,以及对角的运算的理解,了解角之间可以进行加减运算;一个角可以用其他角的和或差来表示.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,已知△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B点和C点在AE的异侧,BD⊥AE于D点,CE⊥AE与E点.
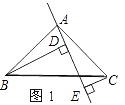
(1)求证:BD=DE+CE
(2)若直线AE绕点A旋转到图2所示的位置时(BD<CE)其余条件不变,问BD 与DE,CE的关系如何?请予以证明.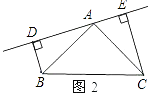
(3)若直线AE绕点A旋转到图3所示的位置时(BD>CE)其余条件不变,问BD 与DE,CE的关系如何?直接写出结果,不需证明.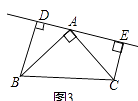
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF,下列结论错误的是( )
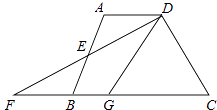
A.△ADE≌△BFE
B.AD+BG=DG
C.连接EG,EG∥DC
D.连接EG,EG⊥DF -
科目: 来源: 题型:
查看答案和解析>>【题目】一次智力测验,有20道选择题.评分标准是:对1题给5分,错1题扣2分,不答题不给分也不扣分.小明有两道题未答.至少答对几道题,总分才不会低于60分.则小明至少答对的题数是( )
A.11道 B。12题 C.13题 D.14题
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(x-2,3)与点B(x+4,y-5)关于原点对称,则xy的值是( )
A.2B.-2C.1D.-1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,太阳光线AC和AC是平行的,同一时刻两个建筑物在太阳下的影子一样长,那么建筑物是否一样高?请说明理由.
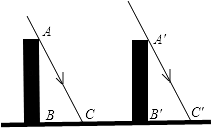
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的内接△ABC的外角∠ACE的平分线交⊙O于点D.DF⊥AC,垂足为F,DE⊥BC,垂足为E.给出下列4个结论:①CE=CF;②∠ACB=∠EDF;③DE是⊙O的切线;④
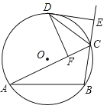
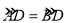 .其中一定成立的是( )
.其中一定成立的是( )A.①②③ B.②③④ C.①③④ D.①②④
相关试题

