【题目】阅读材料并回答问题:
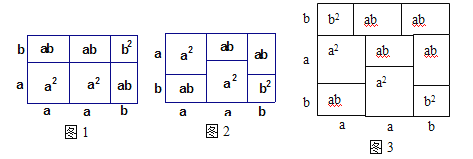
我们知道,乘法公式可以用平面几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示,如:![]() ,就可以用图1或图2等图形的面积表示.
,就可以用图1或图2等图形的面积表示.
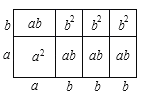
(1)请写出图3所表示的代数恒等式: ;
(2)试画一个几何图形,使它的面积表示:![]() ;
;
(3)请仿照上述方法另写一个含有![]() ,
,![]() 的代数恒等式,并画出与它对应的几何图形.
的代数恒等式,并画出与它对应的几何图形.
参考答案:
【答案】(1)![]() ;(2)答案见试题解析;(3)答案见试题解析.
;(2)答案见试题解析;(3)答案见试题解析.
【解析】
试题(1)根据长方形的面积=长×宽=![]() ,长方形的面积还可以把几个小图形的面积相加,即
,长方形的面积还可以把几个小图形的面积相加,即![]() =
=![]() ;
;
(2)根据等式左边,知道长方形的长和宽,等式右边知道每种基本图形的个数,即可画出图形;
(3)根据所写等式画出图形即可.
试题解析:(1)![]() =
=![]() ;
;
(2)如图,答案不唯一;
(3)恒等式是![]() =
=![]() ,如图所示.(答案不唯一)
,如图所示.(答案不唯一)
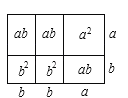
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解不等式2(4x-1)≥5x-8,并把它的解集在数轴上表示出来.

(2)如图,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别是A(-3,0),B(-6,-2)C(-2,-5).将△ABC向上平移3个单位长度,再向右平移5个单位长度,得到△A1B1C1.
①在平面直角坐标系xOy中画出△A1B1C1.
②求△A1B1C1的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列多项式分解因式
(1) 8a3b2-12ab3c (2)2x3-4x2+2x (3)
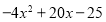 (4)(ab+a)+(b+1) (5)
(4)(ab+a)+(b+1) (5)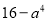
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,然后解答后面的问题:
利用完全平方公式
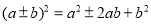 ,通过配方可对
,通过配方可对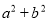 进行适当的变形,如
进行适当的变形,如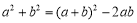 或
或 ,从而使某些问题得到解决,
,从而使某些问题得到解决,例:已知
 ,
,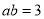 .求
.求 的值.
的值.解:
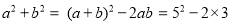 =19
=19问题:已知:
 ,求下列代数式的值.
,求下列代数式的值.(1)
 ;
;(2)
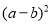 .
.(3)已知
 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】解放中学为了了解学生对新闻、体育、动画、娱乐四类电视节目的喜爱程度,随机抽取了部分学生进行调查(每人限选1项),现将调查结果绘制成如下两幅不完整的统计图,根据图中所给的信息解答下列问题.
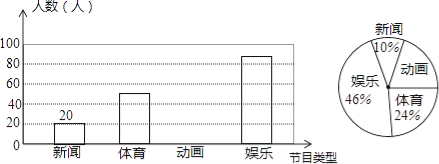
(1)喜爱动画的学生人数和所占比例分别是多少?
(2)请将条形统计图补充完整;
(3)若该校共有学生1000人,依据以上图表估计该校喜欢体育的人数约为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则Bn的坐标是( )

A.(2n﹣1,2n﹣1)B.(2n﹣1+1,2n﹣1)
C.(2n﹣1,2n﹣1)D.(2n﹣1,n)
-
科目: 来源: 题型:
查看答案和解析>>【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄
清理养鱼网箱人数/人
清理捕鱼网箱人数/人
总支出/元
A
15
9
57000
B
10
16
68000
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
相关试题

