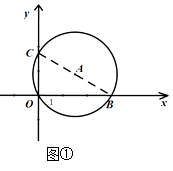
【题目】如图①,在平面直角坐标系中,直径为 ![]() 的⊙A经过坐标系原点O(0,0),与x轴交于点B,与y轴交于点C(0,
的⊙A经过坐标系原点O(0,0),与x轴交于点B,与y轴交于点C(0, ![]() ).
).
(1)求点B的坐标;
(2)如图②,过点B作⊙A的切线交直线OA于点P,求点P的坐标;
(3)过点P作⊙A的另一条切线PE,请直接写出切点E的坐标.
参考答案:
【答案】
(1)解:如图①,连接 ![]() .
.
∵ ![]() ,
,
∴ ![]() 是⊙
是⊙ ![]() 的直径.
的直径.
∴ ![]() ,
,
∵ ![]() ,
,
∴ ![]() .
.
∴ ![]() .
.
∴ ![]() .
.
(2)解:如图②,过点 ![]() 作
作 ![]() 轴于点
轴于点 ![]() .
.
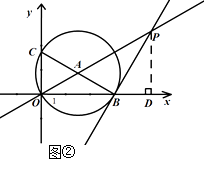
∵ ![]() 为⊙
为⊙ ![]() 的切线,
的切线,
∴ ![]() .
.
在Rt ![]() 中,
中, ![]() ,
, ![]() ,
,
∴ ![]() .
.
∴ ![]() .
.
∴ ![]() .
.
∴ ![]() .
.
∴ ![]() .
.
在Rt ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
,
∴ ![]() ,
, ![]() .
.
∵ ![]() ,
,
∴ ![]() .
.
∴ ![]() .
.
(3)解: ![]()
【解析】(1)利用90度圆周角所对的弦是直径,可求出OB即能得出B坐标;(2)先通过P作x轴的垂线构造出横纵坐标对应的线段,利用切线的性质定理和锐角三角函数,求出坐标;(3)如图,利用切线的性质定理和切线长定理得出∠ EPA=30度,PE于x轴平行,连接AE ,求出EF、OF即可求出坐标.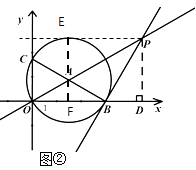
【考点精析】本题主要考查了切线的性质定理的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:线段AB.
(1)尺规作图:作线段AB的垂直平分线l,与线段AB交于点D;(保留作图痕迹,不写作法)
(2)在(1)的基础上,点C为l上一个动点(点C不与点D重合),连接CB,过点A作AE⊥BC,垂足为点E.
①当垂足E在线段BC上时,直接写出∠ABC度数的取值范围.
②若∠B=60,求证:
 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段
 的最小覆盖圆就是以线段
的最小覆盖圆就是以线段  为直径的圆.
为直径的圆.
(1)请分别作出图①中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);
(2)三角形的最小覆盖圆有何规律?请直接写出你所得到的结论(不要求证明);
(3)某城市有四个小区 (其位置如图②所示),现拟建一个手机信号基站,为了使这四个小区居民的手机都能有信号,且使基站所需发射功率最小(距离越小,所需功率越小),此基站应建在何处?请写出你的结论并说明研究思路.
(其位置如图②所示),现拟建一个手机信号基站,为了使这四个小区居民的手机都能有信号,且使基站所需发射功率最小(距离越小,所需功率越小),此基站应建在何处?请写出你的结论并说明研究思路.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境
在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.
操作发现
(1)如图(1),小明把三角尺的60°角的顶点G放在CD上,若∠2=2∠1,求∠1的度数;
(2)如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC之间的数量关系;
结论应用
(3)如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若∠AEG=α,则∠CFG等于______(用含α的式子表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】在等边△ABC中.
(1)如图1,P,Q是BC边上两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②求证:PA=PM.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是本地区一种产品30天的销售图象,图1是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图2是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是( )

A. 第24天的销售量为200件 B. 第10天销售一件产品的利润是15元
C. 第12天与第30天这两天的日销售利润相等 D. 第30天的日销售利润是750元
相关试题

