Question

【题目】已知：线段AB.

（1）尺规作图：作线段AB的垂直平分线l，与线段AB交于点D；（保留作图痕迹，不写作法）

（2）在（1）的基础上，点C为l上一个动点(点C不与点D重合)，连接CB，过点A作AE⊥BC，垂足为点E.

①当垂足E在线段BC上时，直接写出∠ABC度数的取值范围.

②若∠B=60，求证：.

Answer 1

【答案】（1）见解析（2）①45°≤∠ABC＜90°②证明见解析

【解析】

（1）根据题意作图即可；

（2）①连接AC．由CD是AB的垂直平分线，得到AC=BC，由等边对等角得到∠CAB=∠ABC．由于AE⊥BC，得到∠AEB=90°，由三角形内角和定理得到∠EAB+∠ABC =90°，再由∠ABC =∠CAB≥∠EAB，得到∠ABC≥45°，显然∠ABC＜90°，即可得出结论；

②连接AC．由CD是AB的垂直平分线，得到．然后通过证明△ABC是等边三角形，即可得出结论．

（1）按要求作图：

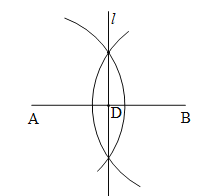
（2）①连接AC．

∵CD是AB的垂直平分线，∴AC=BC，∴∠CAB=∠ABC．

∵AE⊥BC，∴∠AEB=90°，∴∠EAB+∠ABC =90°．

∵∠ABC =∠CAB≥∠EAB，∴2∠ABC≥90°，∴∠ABC≥45°，显然∠ABC＜90°，∴45°≤∠ABC＜90．

②连接AC．

∵CD是AB的垂直平分线，∴，AC=BC．

∵∠B=60，∴△ABC是等边三角形，∴BC=AB，∴．