【题目】在平面直角坐标系xOy中,抛物线![]() 经过点(2,3),对称轴为直线x =1.
经过点(2,3),对称轴为直线x =1.
(1)求抛物线的表达式;
(2)如果垂直于y轴的直线l与抛物线交于两点A(![]() ,
, ![]() ),B(
),B(![]() ,
, ![]() ),其中
),其中![]() ,
, ![]() ,与y轴交于点C,求BC
,与y轴交于点C,求BC![]() AC的值;
AC的值;
(3)将抛物线向上或向下平移,使新抛物线的顶点落在x轴上,原抛物线上一点P平移后对应点为点Q,如果OP=OQ,直接写出点Q的坐标.
参考答案:
【答案】(1)![]() ;(2)BC-AC=2;(3)点Q的坐标为(
;(2)BC-AC=2;(3)点Q的坐标为(![]() )或(
)或(![]() ).
).
【解析】试题分析:(1)由抛物线![]() 经过点(2,3),对称轴为直线x =1,利用待定系数法即可得;
经过点(2,3),对称轴为直线x =1,利用待定系数法即可得;
(2)如图,设l与对称轴交于点M,根据抛物线的对称性,可知AM=BM, AM=AC+CM,BC=BM+CM,推导即可得;
(3)由OP=OQ可知P、Q两点关于x轴对称,求出平移后的解析式,表示出P、Q的坐标,根据关于x轴对称的点的性质即可求得 .
试题解析:(1)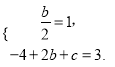 ,解得
,解得![]() ,
,
∴![]() ;
;
(2)如图,设l与对称轴交于点M,则有CM=1,
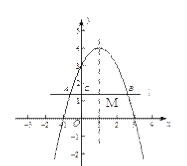
由抛物线的对称性可得,BM= AM,
又∵BC=BM+CM, AM=AC+CM,
∴BC-AC= BM+MC-AC= AM+MC-AC= AC+CM+MC-AC=2CM=2;
(3)![]() =-(x-1)2+4,
=-(x-1)2+4,
所以平移后的抛物线解析式为: ![]() -4=-x2+2x-1,
-4=-x2+2x-1,
设P(m,-m2+2m+3),则平移后对应点Q(m,-m2+2m-1),
因为OP=OQ,所以P、Q两点关于x轴对称,
所以:(-m2+2m+3)+(-m2+2m-1)=0,
解得:m1=![]() ,m2=
,m2=![]() ,
,
所以:点Q的坐标为(![]() )或(
)或(![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是矩形ABCD边AB上一动点(不与点B重合),过点E作EF⊥DE交BC于点F,连接DF.已知AB = 4cm,AD = 2cm,设A,E两点间的距离为xcm,△DEF面积为ycm2.小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.

下面是小明的探究过程,请补充完整:
(1)确定自变量x的取值范围是 ;
(2)通过取点、画图、测量、分析,得到了x与y的几组值,如下表:
x/cm
0
0.5
1
1.5
2
2.5
3
3.5
…
y/cm2
4.0
3.7
3.9
3.8
3.3
2.0
…
(说明:补全表格时相关数值保留一位小数)
(3)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(4)结合画出的函数图象,解决问题:当△DEF面积最大时,AE的长度为 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店需要购进甲、乙两种商品共180件其进价和售价如表:(注:获利=售价进价)
(1)若商店计划销售完这批商品后能获利1240元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于5040元,且销售完这批商品后获利多于1312元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.

-
科目: 来源: 题型:
查看答案和解析>>【题目】求不等式(2x﹣1)(x+3)>0的解集.
解:根据“同号两数相乘,积为正”可得:①
 或 ②
或 ② .
.解①得x>
 ;解②得x<﹣3.
;解②得x<﹣3.∴不等式的解集为x>
 或x<﹣3.
或x<﹣3.请你仿照上述方法解决下列问题:
(1)求不等式(2x﹣3)(x+1)<0的解集.
(2)求不等式
 ≥0的解集.
≥0的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,a),B(b,a),且a,b满足(a﹣3)2+|b﹣6|=0,现同时将点A,B分别向下平移3个单位,再向左平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=
 S四边形ABCD?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
S四边形ABCD?若存在这样一点,求出点M的坐标,若不存在,试说明理由;(3)点P是直线BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合),直接写出∠BAP,∠DOP,∠APO之间满足的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角三角形纸片的两直角边长分别为6、8,按如图那样折叠,使点A与点B重合,折痕为DE,则S△BCE:S△BDE等于( )
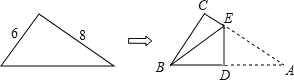
A.2:5 B.14:25 C.16:25 D.4:21
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAD=90°,AB=AD,CB=CD,一个以点C为顶点的45°角绕点C旋转,角的两边与BA,DA交于点M,N,与BA,DA的延长线交于点E,F,连接AC.
(1)在∠FCE旋转的过程中,当∠FCA=∠ECA时,如图1,求证:AE=AF;
(2)在∠FCE旋转的过程中,当∠FCA≠∠ECA时,如图2,如果∠B=30°,CB=2,用等式表示线段AE,AF之间的数量关系,并证明.

相关试题

