【题目】若二次函数y=ax2+bx+c(a≠0)的图象于x轴的交点坐标分别为(x1 , 0),(x2 , 0),且x1<x2 , 图象上有一点M(x0 , y0)在x轴下方,对于以下说法: ①b2﹣4ac>0;
②x=x0是方程ax2+bx+c=y0的解;
③x1<x0<x2
④a(x0﹣x1)(x0﹣x2)<0;
⑤x0<x1或x0>x2 ,
其中正确的有( )
A.①②
B.①②④
C.①②⑤
D.①②④⑤
参考答案:
【答案】B
【解析】解:①∵二次函数y=ax2+bx+c(a≠0)的图象于x轴的交点坐标分别为(x1 , 0),(x2 , 0),且x1<x2 , ∴方程ax2+bx+c=0有两个不相等的实数根,
∴△=b2﹣4ac>0,①正确;②∵图象上有一点M(x0 , y0),
∴a ![]() +bx0+c=y0 ,
+bx0+c=y0 ,
∴x=x0是方程ax2+bx+c=y0的解,②正确;③当a>0时,∵M(x0 , y0)在x轴下方,
∴x1<x0<x2;
当a<0时,∵M(x0 , y0)在x轴下方,
∴x0<x1或x0>x2 , ③错误;④∵二次函数y=ax2+bx+c(a≠0)的图象于x轴的交点坐标分别为(x1 , 0),(x2 , 0),
∴y=ax2+bx+c=a(x﹣x1)(x﹣x2),
∵图象上有一点M(x0 , y0)在x轴下方,
∴y0=a(x0﹣x1)(x0﹣x2)<0,④正确;⑤根据③即可得出⑤错误.
综上可知正确的结论有①②④.
故选B.
【考点精析】解答此题的关键在于理解二次函数图象以及系数a、b、c的关系的相关知识,掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c),以及对抛物线与坐标轴的交点的理解,了解一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.

(1)求DE的长;
(2)求△ADB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,分别以AB、AD为边向外作等边△ABE,△ADF,延长CB交AE于点G,点G落在点A、E之间,连接EF、CF.则以下四个结论:①CG⊥AE;②△CDF≌△EBC;③∠CDF =∠EAF;④△ECF是等边三角形.其中一定正确的是 .(把正确结论的序号都填上)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省( )

A.1元
B.2元
C.3元
D.4元 -
科目: 来源: 题型:
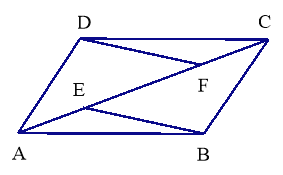
查看答案和解析>>【题目】已知:如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.
求证:(1)△ABE≌△CDF;(2)BE∥DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设x1、x2是一元二次方程x2+4x﹣3=0的两个根,2x1(x22+5x2﹣3)+a=2,则a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.

(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
相关试题

