【题目】已知:如图1,点![]() 、
、![]() 、
、![]() 依次在直线
依次在直线![]() 上,现将射线
上,现将射线![]() 绕点
绕点![]() 沿顺时针方向以每秒
沿顺时针方向以每秒![]() 的速度旋转,同时射线
的速度旋转,同时射线![]() 绕点
绕点![]() 沿逆时针方向以每秒
沿逆时针方向以每秒![]() 的速度旋转,如图
的速度旋转,如图![]() ,设旋转时间为
,设旋转时间为![]() (
(![]() 秒
秒![]() 秒).
秒).
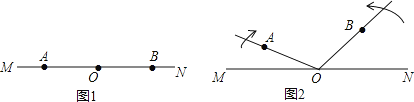
(1)用含![]() 的代数式表示
的代数式表示![]() 的度数.
的度数.
(2)在运动过程中,当![]() 第二次达到
第二次达到![]() 时,求
时,求![]() 的值.
的值.
(3)在旋转过程中是否存在这样的![]() ,使得射线
,使得射线![]() 是由射线
是由射线![]() 、射线
、射线![]() 、射线
、射线![]() 中的其中两条组成的角(指大于
中的其中两条组成的角(指大于![]() 而不超过
而不超过![]() 的角)的平分线?如果存在,请直接写出
的角)的平分线?如果存在,请直接写出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
参考答案:
【答案】(1)∠MOA=2t;(2)40秒;(3)t的值分别为18、22.5、36、67.5秒.
【解析】
(1)∠AOM的度数等于OA旋转速度乘以旋转时间;
(2)当∠AOB第二次达到60°时,射线OB在OA的左侧,根据∠AOM+∠BON-∠MON=60°列方程求解可得;
(3)射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角的平分线有三种情况:
①OB平分∠AOM时,根据![]() ∠AOM=∠BOM,列方程求解,
∠AOM=∠BOM,列方程求解,
②OB平分∠MON时,根据∠BOM=![]() ∠MON,列方程求解,
∠MON,列方程求解,
③OB平分∠AON时,根据∠BON=![]() ∠AON,列方程求解.
∠AON,列方程求解.
(1)由题意得:∠MOA=2t;
(2)如图,

根据题意知:∠AOM=2t,∠BON=4t,
当∠AOB第二次达到60°时,∠AOM+∠BON-∠MON=60°,
即2t+4t-180=60,解得:t=40,
故t=40秒时,∠AOB第二次达到60°;
(3)射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角的平分线有以下三种情况:
①OB平分∠AOM时,
∵![]() ∠AOM=∠BOM,
∠AOM=∠BOM,
∴t=180-4t,
解得:t=36;
②OB平分∠MON时,
∵∠BOM=![]() ∠MON,即∠BOM=90°,
∠MON,即∠BOM=90°,
∴4t=90,或4t-180=90,
解得:t=22.5,或t=67.5;
③OB平分∠AON时,
∵∠BON=![]() ∠AON,
∠AON,
∴4t=![]() (180-2t),
(180-2t),
解得:t=18;
综上,当t的值分别为18、22.5、36、67.5秒时,射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角的平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC与BD相交于点O,
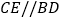 ,
,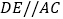 .若
.若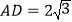 ,
, ,则四边形OCED的面积为___.
,则四边形OCED的面积为___.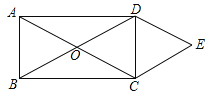
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.
(1)求抛物线的解析式;
(2)点D在y轴上,且∠BDO=∠BAC,求点D的坐标;
(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列代数式书写规范的是( )
A. a÷3B. a8C. 5aD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线OM上有三点A、B、C,OC=45cm, BC=15cm, AB=30cm,已知动点P、Q同时运动,其中动点P从点O出发沿OM方向以速度2cm/s匀速运动,动点Q从点C出发沿CA方向匀速运动,当点Q运动到点A时,点Q停止运动(点P继续运动).设运动时间为t秒.

(1)求点P运动到点B所用的时间;
(2)若点Q运动速度为每秒1cm,经过多少秒时,点P和点Q的距离为30cm;
(3)当PA=2PB时,点Q恰好在线段AB的三等分点的位置,求点Q的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中小学时期是学生身心变化最为明显的时期,这个时期孩子们的身高变化呈现一定的趋势,7~15岁期间生子们会经历一个身高发育较迅速的阶段,我们把这个年龄阶段叫做生长速度峰值段,小明通过上网查阅《2016年某市儿童体格发育调查表》,了解某市男女生7~15岁身高平均值记录情况,并绘制了如下统计图,并得出以下结论:
①10岁之前,同龄的女生的平均身高一般会略高于男生的平均身高;
②10~12岁之间,女生达到生长速度峰值段,身高可能超过同龄男生;
③7~15岁期间,男生的平均身高始终高于女生的平均身高;
④13~15岁男生身高出现生长速度峰值段,男女生身高差距可能逐渐加大.
以上结论正确的是( )
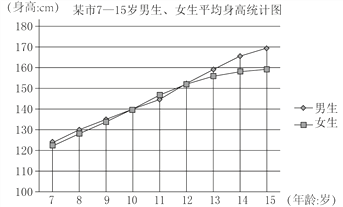
A. ①③ B. ②③ C. ②④ D. ③④
-
科目: 来源: 题型:
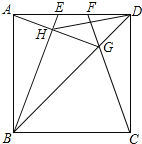
查看答案和解析>>【题目】如图,E、F是正方形ABCD的边AD上的两个动点,满足AE=DF.连接CF交BD于G,连接BE交AG于H.已知正方形ABCD的边长为4cm,解决下列问题:
(1)求证:BE⊥AG;
(2)求线段DH的长度的最小值.
相关试题

