【题目】例:解方程![]()
解:设![]() ,则
,则![]() ,∴原方程可化为:
,∴原方程可化为:![]() ,解得
,解得![]()
当y=3时,![]() ,
,![]() ,当y=4时,
,当y=4时,![]() .
.
∴原方程有四个根是:![]() .
.
以上方法叫换元法,达到了降次的目的,体现了数学的转化思想,运用上述方法解答下列问题.
(1)解方程:![]() ;
;
(2)已知a、b、c是Rt△ABC的三边(c为斜边),![]() ,且a、b满足
,且a、b满足![]() ,试求Rt△ABC的周长.
,试求Rt△ABC的周长.
参考答案:
【答案】(1)、x1,2=![]() ,x3,4=
,x3,4=![]() ;(2)、12
;(2)、12
【解析】
试题分析:(1)、设y=x2+x-2,然后求出y的值,然后根据y的值分别求出x的值,得出方程的解;(2)、y=a2+b2,然后求出y的值,得出C的值,根据面积求出ab=12,然后根据完全平方公式得出a+b的值,从而得出三角形的周长.
试题解析:(1)、设y=x2+x-2,则y2﹣y-2=0,解得y1=-1,y2=2,
当x2+x-2=-1 即x2+x﹣1=0时,解得:x=![]() ;
;
当x2+x-2=2 即x2+x﹣4=0时,解得:x=![]() ;
;
综上所述,原方程的解为x1,2=![]() ,x3,4=
,x3,4=![]() ;
;
(2)、![]() ,设y=a2+b2,则y2﹣21y﹣100=0,整理,得
,设y=a2+b2,则y2﹣21y﹣100=0,整理,得
(y﹣25)(y+4)=0,解得y1=5,y2=﹣4(舍去),故a2+b2=25.C=5,
又∵![]() ,
,![]() ,
,![]() ,又a2+b2=25,(a+b)2-2ab=25, (a+b)2=49, a+b=7,
,又a2+b2=25,(a+b)2-2ab=25, (a+b)2=49, a+b=7,
∴a+b+c=12 即△ABC的周长为12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B在一直线上,小明从点A出发沿AB方向匀速前进,4秒后走到点D,此时他(CD)在某一灯光下的影长为AD,继续沿AB方向以同样的速度匀速前进4秒后到点F,此时他(EF)的影长为2米,然后他再沿AB方向以同样的速度匀速前进2秒后达点H,此时他(GH)处于灯光正下方.
(1)请在图中画出光源O点的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法);
(2)求小明沿AB方向匀速前进的速度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】周老师在一次“探究性学习”课中,设计了如下数表:
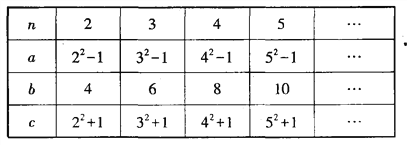
(1)请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:
a=__ _____;b=___ ____;c=___ ____;
(2)猜想:以a,b,c为边长的三角形是否是直角三角形?证明你的猜想.
(3)、显然,满足这样关系的整数a、b、c我们把它叫做 数,请再写一组这样的数 (不同于表格中已出现的数组)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. x2x4=x8 B. (﹣x3)2=x6 C. (xy)2=xy2 D. x6÷x2=x3
-
科目: 来源: 题型:
查看答案和解析>>【题目】PM2.5是指大气中直径≤0.0000025米的颗粒物,将0.0000025用科学记数法表示为( )
A.2.5×10﹣7
B.2.5×10﹣6
C.25×10﹣7
D.0.25×10﹣5 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣a2)34a (2)2x(x+1)+(x+1)2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的是( )
A. 若a=b,则a+c=b+c B. 若ac=bc,则a=b C. 若|a|=|b|,则a=b D. 若a2=b2,则a=b
相关试题

