【题目】如图,为了测量出楼房AC的高度,从距离楼底C处60 ![]() 米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:
米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1: ![]() 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈
的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈ ![]() ,计算结果用根号表示,不取近似值).
,计算结果用根号表示,不取近似值).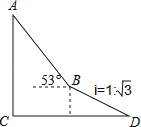
参考答案:
【答案】解:如图作BN⊥CD于N,BM⊥AC于M.
在RT△BDN中,BD=30,BN:ND=1: ![]() ,
,
∴BN=15,DN=15 ![]() ,
,
∵∠C=∠CMB=∠CNB=90°,
∴四边形CMBN是矩形,
∴CM=BM=15,BM=CN=60 ![]() ﹣15
﹣15 ![]() =45
=45 ![]() ,
,
在RT△ABM中,tan∠ABM= ![]() =
= ![]() ,
,
∴AM=27 ![]() ,
,
∴AC=AM+CM=15+27 ![]() .
.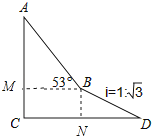
【解析】如图作BN⊥CD于N,BM⊥AC于M,先在RT△BDN中求出线段BN,在RT△ABM中求出AM,再证明四边形CMBN是矩形,得CM=BN即可解决问题.本题考查解直角三角形、仰角、坡度等概念,解题的关键是添加辅助线构造直角三角形,记住坡度的定义,属于中考常考题型.
【考点精析】本题主要考查了关于坡度坡角问题和关于仰角俯角问题的相关知识点,需要掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA;仰角:视线在水平线上方的角;俯角:视线在水平线下方的角才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
(1)求证:四边形OCED是矩形;
(2)若CE=1,DE=2,ABCD的面积是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=-3x+3与x轴,y轴分别交于A,B,两点,以AB为边在第一象限内作正方形ABCD,点D在反比例函数y=
 (k≠0)的图象上.
(k≠0)的图象上.(1)求k的值;
(2)若将正方形沿x轴负方向平移m个单位长度后,点C恰好落在该反比例函数的图象上,则m的值是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】禁渔期间,我渔政船在A处发现正北方向B处有一艘可以船只,测得A、B两处距离为200海里,可疑船只正沿南偏东45°方向航行,我渔政船迅速沿北偏东30°方向前去拦截,经历4小时刚好在C处将可疑船只拦截.求该可疑船只航行的平均速度(结果保留根号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的高,AE、BF分别是∠BAC,∠ABC的平分线,∠DAC=20,
⑴若∠ABC=60°,求∠EAD的度数;
⑵AE、BF相交于点G,求∠AGB的度数。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据:
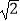 ≈1.414,
≈1.414, 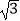 ≈1.732)
≈1.732)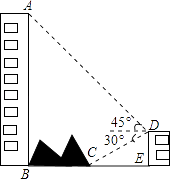
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知线段AB、CD相交于点O,连接AC、BD,我们把形如图①的图形称之为“8字形”.
(1)如图①,若∠A=∠D,判断∠C与∠B的数量关系,并说明理由;
(2)如图②,∠CAB和∠BDC的平分线AP和DP相交于点P,并且与CD、AB分别相交于M、N,试解答下列问题:
①仔细观察,在图②中有 个“8字形”;
②∠B=80°,∠C=100°,求∠P的度数.

相关试题

