【题目】禁渔期间,我渔政船在A处发现正北方向B处有一艘可以船只,测得A、B两处距离为200海里,可疑船只正沿南偏东45°方向航行,我渔政船迅速沿北偏东30°方向前去拦截,经历4小时刚好在C处将可疑船只拦截.求该可疑船只航行的平均速度(结果保留根号).
参考答案:
【答案】解:过点C作CD⊥AB,垂足为点D,设BD=x海里,则AD=(200﹣x)海里,
∵∠ABC=45°,
∴BD=CD=x,
∵∠BAC=30°,
∴tan30°= ![]() ,
,
在Rt△ACD中,则CD=ADtan30°= ![]() (200﹣x),
(200﹣x),
则x= ![]() (200﹣x),
(200﹣x),
解得,x=100 ![]() ﹣100,
﹣100,
即BD=100 ![]() ﹣100,
﹣100,
在Rt△BCD中,cos45°= ![]() ,
,
解得:BC=100 ![]() ﹣100
﹣100 ![]() ,
,
则100 ![]() ﹣100
﹣100 ![]() ÷4=25(
÷4=25( ![]() ﹣
﹣ ![]() )(海里/时),
)(海里/时),
则该可疑船只的航行速度约为25( ![]() ﹣
﹣ ![]() )海里/时.
)海里/时.
【解析】先过点C作CD⊥AB,垂足为点D,设BD=x海里,得出AD=(200﹣x)海里,在Rt△BCD中,根据tan45°= ![]() ,求出CD,再根据BD=CD求出BD,在Rt△BCD中,根据cos45°=
,求出CD,再根据BD=CD求出BD,在Rt△BCD中,根据cos45°= ![]() ,求出BC,从而得出答案.此题考查了解直角三角形的应用,用到的知识点是方向角含义、三角函数的定义,关键是根据题意画出图形,构造直角三角形.
,求出BC,从而得出答案.此题考查了解直角三角形的应用,用到的知识点是方向角含义、三角函数的定义,关键是根据题意画出图形,构造直角三角形.
【考点精析】关于本题考查的关于方向角问题,需要了解指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知函数
 的图象与
的图象与 轴、
轴、 轴分别交于点
轴分别交于点 ,与函数
,与函数 的图象交于点
的图象交于点 ,点
,点 的横坐标为2.在
的横坐标为2.在 轴上有一点
轴上有一点 (其中
(其中 ),过点
),过点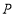 作
作 轴的垂线,分别交函数
轴的垂线,分别交函数 和
和 的图象于点
的图象于点 .
.(1)求点
 的坐标;
的坐标;(2)若四边形
 是平行四边形,求
是平行四边形,求 的值.
的值.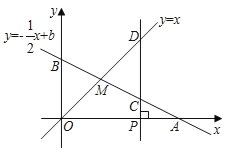
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
(1)求证:四边形OCED是矩形;
(2)若CE=1,DE=2,ABCD的面积是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=-3x+3与x轴,y轴分别交于A,B,两点,以AB为边在第一象限内作正方形ABCD,点D在反比例函数y=
 (k≠0)的图象上.
(k≠0)的图象上.(1)求k的值;
(2)若将正方形沿x轴负方向平移m个单位长度后,点C恰好落在该反比例函数的图象上,则m的值是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了测量出楼房AC的高度,从距离楼底C处60
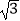 米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:
米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1: 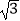 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈
的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈  ,计算结果用根号表示,不取近似值).
,计算结果用根号表示,不取近似值).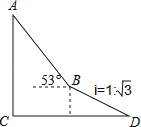
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的高,AE、BF分别是∠BAC,∠ABC的平分线,∠DAC=20,
⑴若∠ABC=60°,求∠EAD的度数;
⑵AE、BF相交于点G,求∠AGB的度数。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据:
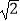 ≈1.414,
≈1.414, 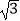 ≈1.732)
≈1.732)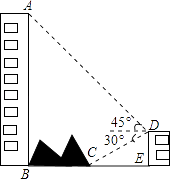
相关试题

