【题目】大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() 来表示
来表示![]() 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:
的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:
∵![]() ,即
,即![]() ,∴
,∴![]() 的整数部分为2,小数部分为
的整数部分为2,小数部分为![]() .
.
请解答:(1)如果![]() 的小数部分为a,
的小数部分为a,![]() 的整数部分为b,求
的整数部分为b,求![]() 的值;
的值;
(2)已知:![]() ,其中x是整数,且0<y<1.
,其中x是整数,且0<y<1.
求:①x、y的值;②x﹣y的相反数.
参考答案:
【答案】(1)1;(2)①x=11,y=![]() -1;②
-1;②![]() -12.
-12.
【解析】
(1)依题意易得![]() 的整数部分为2,小数部分a=
的整数部分为2,小数部分a=![]() -2;
-2;![]() 的整数部分为3,所以b=3;
的整数部分为3,所以b=3;
(2) 依题意易得![]() 的整数部分为1,所以10+
的整数部分为1,所以10+![]() 的整数部分为11,∴x=11.
的整数部分为11,∴x=11.
(1)根据题意得:a=![]() -2,b=3,则a+b-
-2,b=3,则a+b-![]() =1;
=1;
(2)①∵x为整数,10+![]() =x+y,且0<y<1,∴x=11,y=
=x+y,且0<y<1,∴x=11,y=![]() -1;
-1;
②x-y的相反数为-(x-y)=-x+y=![]() -12.
-12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系xOy中,一直线y=2x+b经过点A(-1,0)与y轴正半轴交于B点,在x轴正半轴上有一点D,且OB=OD,过D点作DC⊥x轴交直线y=2x+b于C点,反比例函数y=
 (x>O)经过点C.
(x>O)经过点C.
(1)求b,k的值;
(2)求△BDC的面积;
(3)在反比例函数y=
 (x>0)的图象上找一点P(异于点C),使△BDP与△BDC的面积相等,求出P点坐标.
(x>0)的图象上找一点P(异于点C),使△BDP与△BDC的面积相等,求出P点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是等边三角形,D为边AC的中点,AE⊥EC,BD=EC.
(1)求证:△BDA≌△CEA;
(2)请判断△ADE是什么三角形,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=6,BC=8.
(1)求对角线AC的长;
(2)点E是线段CD上的一点,把△ADE沿着直线AE折叠.点D恰好落在线段AC上,与点F重合,求线段DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC中,CD⊥AB于D,且BD : AD : CD=2 : 3 : 4,
(1)求证:AB=AC;
(2)已知S△ABC=40cm2,如图2,动点M从点B出发以每秒1cm的速度沿线段BA向点A 运动,同时动点N从点A出发以相同速度沿线段AC向点C运动,当其中一点到达终点时整个运动都停止. 设点M运动的时间为t(秒),
①若△DMN的边与BC平行,求t的值;
②若点E是边AC的中点,问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图2.已知铁环的半径为25 cm,设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=
 .
.(1)求点M离地面AC的高度BM;
(2)设人站立点C与点A的水平距离AC=55 cm,求铁环钩MF的长度.
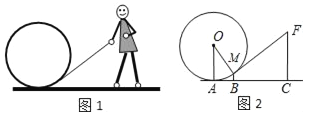
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,点P(2,6),B(4,0),若以PB为边在第一象限内作等腰直角三角形△PBC,则点C的坐标为_______.

相关试题

