【题目】如图,平面直角坐标系中,点P(2,6),B(4,0),若以PB为边在第一象限内作等腰直角三角形△PBC,则点C的坐标为_______.

参考答案:
【答案】(10,2)或(6,4)或(8,8).
【解析】
以PB为边在第一象限内作正方形![]() ,此时正方形的另外两个顶点
,此时正方形的另外两个顶点![]() 、
、![]() 以及正方形对角线的交点
以及正方形对角线的交点![]() 为所求点C,过点P作PM⊥x轴于点M,过点
为所求点C,过点P作PM⊥x轴于点M,过点![]() 作
作![]() ⊥x轴于点N,易证
⊥x轴于点N,易证![]() ,可得M=BN,BM=
,可得M=BN,BM=![]() ,根据点P和点B的坐标可知PM与BM的长度,进而可求
,根据点P和点B的坐标可知PM与BM的长度,进而可求![]() 坐标,结合P点坐标由中点坐标公式可求
坐标,结合P点坐标由中点坐标公式可求![]() 的中点
的中点![]() 的坐标,然后结合点B的坐标用中点坐标公式可求
的坐标,然后结合点B的坐标用中点坐标公式可求![]() 点坐标,进而求得符合条件的三个点C的坐标.
点坐标,进而求得符合条件的三个点C的坐标.

如图所示,过点B作PB的垂线并截取![]() =PB,过点P作PB的垂线并截取
=PB,过点P作PB的垂线并截取![]() =PB,连接
=PB,连接![]() ,则四边形
,则四边形![]() 为正方形,连接
为正方形,连接![]() 、
、![]() 交于点
交于点![]() ,则
,则![]() 、
、![]() 、
、![]() 均为等腰直角三角形,此时
均为等腰直角三角形,此时![]() 、
、![]() 、
、![]() 即为所求的点C.
即为所求的点C.
过点P作PM⊥x轴于点M,过点![]() 作
作![]() ⊥x轴于点N,则∠PMB=
⊥x轴于点N,则∠PMB= ![]() =90°,
=90°,
∵![]() =90°,
=90°,
∴∠PBM+![]() =90°,
=90°,
又∵∠MPB+∠PBM=90°,![]() +
+![]() = 90°,
= 90°,
∴∠MPB=![]() ,∠PBM=
,∠PBM=![]() ,
,
又∵![]() =PB,
=PB,
∴![]() ,
,
∴PM=BN,BM=![]() ,
,
∵P(2,6),B(4,0),
∴PM=6,OM=2,OB=4,
∴BN=6, ![]() =2,
=2,
∴ON=10,
∴点![]() 的坐标为(10,2),
的坐标为(10,2),
∵![]() 为
为![]() 的中点,P(2,6),
的中点,P(2,6),
∴点![]() 的坐标为(6,4),
的坐标为(6,4),
又∵![]() 为
为![]() 的中点,B(4,0),
的中点,B(4,0),
∴点![]() 的坐标为(8,8),
的坐标为(8,8),
故符合题意的点C的坐标为:(10,2)或(6,4)或(8,8).
-
科目: 来源: 题型:
查看答案和解析>>【题目】大家知道
 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用 来表示
来表示 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理,因为 的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:
的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵
 ,即
,即 ,∴
,∴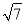 的整数部分为2,小数部分为
的整数部分为2,小数部分为 .
.请解答:(1)如果
 的小数部分为a,
的小数部分为a, 的整数部分为b,求
的整数部分为b,求 的值;
的值;(2)已知:
 ,其中x是整数,且0<y<1.
,其中x是整数,且0<y<1.求:①x、y的值;②x﹣y的相反数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC中,CD⊥AB于D,且BD : AD : CD=2 : 3 : 4,
(1)求证:AB=AC;
(2)已知S△ABC=40cm2,如图2,动点M从点B出发以每秒1cm的速度沿线段BA向点A 运动,同时动点N从点A出发以相同速度沿线段AC向点C运动,当其中一点到达终点时整个运动都停止. 设点M运动的时间为t(秒),
①若△DMN的边与BC平行,求t的值;
②若点E是边AC的中点,问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.

-
科目: 来源: 题型:
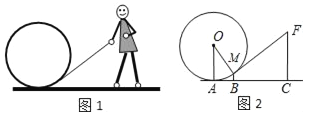
查看答案和解析>>【题目】图1是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图2.已知铁环的半径为25 cm,设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=
 .
.(1)求点M离地面AC的高度BM;
(2)设人站立点C与点A的水平距离AC=55 cm,求铁环钩MF的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工艺品厂生产一种汽车装饰品,每件生产成本为20元,销售价格在30元至80元之间(含30元和80元),销售过程中的管理、仓储、运输等各种费用(不含生产成本)总计50万元,其销售量y(万个)与销售价格(元/个)的函数关系如图所示.
(1)当30≤x≤60时,求y与x的函数关系式;
(2)求出该厂生产销售这种产品的纯利润w(万元)与销售价格x(元/个)的函数关系式;
(3)销售价格应定为多少元时,获得利润最大,最大利润是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC和△BDE是等腰直角三角形,∠ABC=∠DBE=90°,点D在AC上.
(1)求证:△ABD≌△CBE;
(2)若DB=1,求AD2+CD2的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果抛物线C1的顶点在抛物线C2上,同时,抛物线C2的顶点在抛物线C1上,那么,我们称抛物线C1与C2关联.
(1)已知两条抛物线①:y=x2+2x﹣1,②:y=﹣x2+2x+1,判断这两条抛物线是否关联,并说明理由;
(2)抛物线C1:y=
 (x+1)2﹣2,动点P的坐标为(t,2),将抛物线C1绕点P(t,2)旋转180°得到抛物线C2,若抛物线C2与C1关联,求抛物线C2的解析式.
(x+1)2﹣2,动点P的坐标为(t,2),将抛物线C1绕点P(t,2)旋转180°得到抛物线C2,若抛物线C2与C1关联,求抛物线C2的解析式.
相关试题

