【题目】如图,在△ABC中,BO、CO分别是∠ABC、∠ACB的角平分线,求:

(1)若∠A=50°,求∠BOC的度数.
(2)在其他条件不变的情况下,若∠A=n°,则∠A与∠BOC之间有怎样的数量关系?
参考答案:
【答案】(1)115°;(2)∠BOC=90°+![]() ∠A.
∠A.
【解析】试题分析:(1)根据三角形的内角和得到∠ABC+∠ACB=180°-∠A=130°,由于BO、CO分别是△ABC的角∠ABC、∠ACB的平分线,得到∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,根据三角形的内角和即可得到结论;
∠ACB,根据三角形的内角和即可得到结论;
(2)根据∠ABC与∠ACB的平分线相交于点O,得到∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,于是得到∠OBC+∠OCB=
∠ACB,于是得到∠OBC+∠OCB=![]() (∠ABC+∠ACB),根据三角形内角和即可得到结论.
(∠ABC+∠ACB),根据三角形内角和即可得到结论.
试题解析:(1)∵∠A=50°,
∴∠ABC+∠ACB=180°-∠A=130°,
∵BO、CO分别是△ABC的角∠ABC、∠ACB的平分线,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB)=65°,
(∠ABC+∠ACB)=65°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-65°=115°;
(2)∵∠ABC与∠ACB的平分线相交于点O,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB),
(∠ABC+∠ACB),
在△OBC中,
∠BOC=180°-(∠OBC+∠OCB)
=180°-![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
=180°-![]() (180°-∠A)
(180°-∠A)
=90°+![]() ∠A,
∠A,
即∠BOC=90°+![]() ∠A.
∠A.
考点:三角形内角和定理.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中不适合普查而适合抽样调查的是( )
①了解市面上一次性筷子的卫生情况
②了解我校九年级学生身高情况
③了解一批导弹的杀伤范围
④了解全世界网迷少年的性格情况
A、①②③ B、①②④
C、②③④ D、①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】我校九年级(1)班所有学生参加2015年初中毕业生升学体育测试,根据测试评分标准,将他们的成绩进行统计后分为A、B、C、D四等,并绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:

(1)九年级(1)班参加体育测试的学生有 人;
(2)将条形统计图补充完整;
(3)在扇形统计图中,等级B部分所占的百分比是 ,等级C对应的圆心角的度数为 ;
(4)若该校九年级学生共有550人参加体育测试,估计达到A级和B级的学生共有 人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程或方程组
(1)x﹣6=3(2﹣x);
(2)
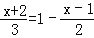 ;
;(3)
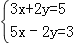 ;
;(4)
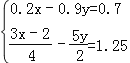 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等腰直角三角形,∠A=90°,点P、Q分别是AB、AC上的一动点,且满足BP=AQ,D是BC的中点.
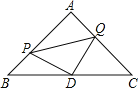
(1)求证:△PDQ是等腰直角三角形;
(2)当点P运动到什么位置时,四边形APDQ是正方形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
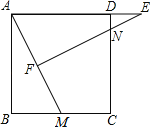
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程(m+1)x2-2x+1=0有实数根,则实数m的取值范围是( )
A、m≥0 B、m≤0 C、m≠1 D、m≤0且m≠-1
相关试题

