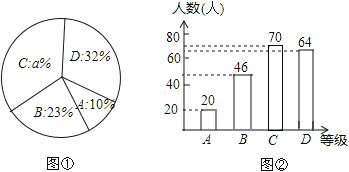
【题目】一家食品公司将一种新研发的食品免费送给一些人品尝,并让每个人按A(不喜欢)、B(一般)、C(比较喜欢)、D(非常喜欢)四个等级对食品进行评价,图1和图2是该公司采集数据后,绘制的两幅不完整的统计图.
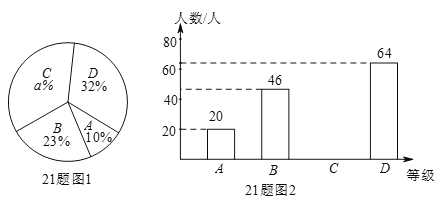
请你根据以上统计图提供的信息,回答下列问题:
(1)本次调查的人数为 人;
(2)图1中,a = ,C等级所占的圆心角的度数为 度;
(3)请直接在图中补全条形统计图.
参考答案:
【答案】解:(1)200。
(2)35;126。
(3)补全统计图如图所示:
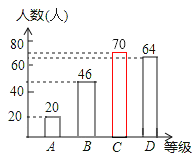
【解析】试题分析:(1)用A的人数与所占的百分比列式计算即可得解;(2)先求出C的人数,再求出百分比即可得到a的值,用C所占的百分比乘以360°计算即可得解;(3)根据计算补全统计图即可.
试题解析:(1)20÷10%=200人;
(2)C的人数为:200-20-46-64=70,所占的百分比为: ![]() ×100%=35%,所以,a=35,所占的圆心角的度数为:35%×360°=126°;
×100%=35%,所以,a=35,所占的圆心角的度数为:35%×360°=126°;
(3)补全统计图如图所示:
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在航线l的两侧分别有观测点A和B,点B到航线l的距离BD为4km,点A位于点B北偏西60°方向且与B相距20km处.现有一艘轮船从位于点A南偏东74°方向的C处,沿该航线自东向西航行至观测点A的正南方向E处.求这艘轮船的航行路程CE的长度.(结果精确到0.1km)(参考数据:
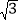 ≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
-
科目: 来源: 题型:
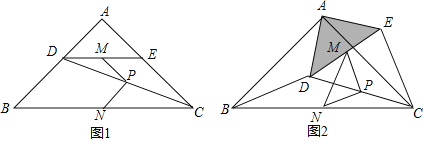
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.
-
科目: 来源: 题型:
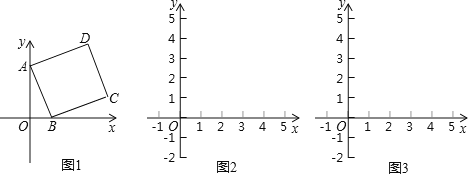
查看答案和解析>>【题目】在平面直角坐标系中,点A的坐标为(0,3),点B和点D的坐标分别为(m,0),(n,4),且m>0,四边形ABCD是矩形.
(1)如图1,当四边形ABCD为正方形时,求m,n的值;
(2)在图2中,画出矩形ABCD,简要说明点C,D的位置是如何确定的,并直接用含m的代数式表示点C的坐标;
(3)探究:当m为何值时,矩形ABCD的对角线AC的长度最短.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=6,AC=3,则BE=( )
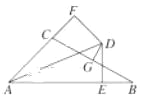
A. 6 B. 3 C. 2 D. 1.5
-
科目: 来源: 题型:
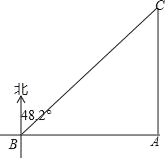
查看答案和解析>>【题目】如图,在一次海警演习中,A、B两地分别同时派出甲、乙两快艇营救一货轮C,已知B地位于A地正西方向相距84海里位置,货轮C位于A地正北方向,位于B地北偏东48.2°方向(所有数据精确到个位,sin48.2°≈0.7,cos48.2°≈0.6,tan48.2°≈1.05)
(1)求A、B两地分别与货轮C的距离;
(2)若乙快艇每小时比甲快艇多行驶20海里,且它们同时达到货轮C位置,求甲、乙快艇的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=2∠B.
(1)作∠ACB的平分线交AB于D(要求用尺规作图,保留作图痕迹,不要求写作法);
(2)若AB=10,AC=6,求△ACD的周长.
相关试题

