【题目】如图,已知∠1+∠2=180°,∠A=∠C,AD平分∠BDF.
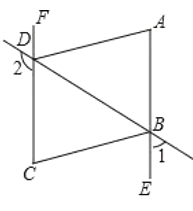
(1)AE与FC的位置关系如何?为什么?
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?
参考答案:
【答案】(1)AE∥FC,理由见解析;(2)AD∥BC,理由见解析;(3)BC平分∠DBE,理由见解析.
【解析】
(1)证明∠1=∠CDB,利用同位角相等,两直线平行即可证得结论;
(2)根据平行线的性质可以证得∠A=∠CBE,然后利用平行线的判定即可证得结论;
(3)根据平行线的性质证明∠EBC=∠CBD即可证得结论.
(1)AE∥FC.
理由如下:
∵∠1+∠2=180°,∠2+∠CDB=180°(邻补角定义),
∴∠1=∠CDB,
∴AE∥FC( 同位角相等两直线平行);
(2)AD∥BC.
理由如下:
∵AE∥CF,
∴∠C=∠CBE(两直线平行,内错角相等),
又∵∠A=∠C,
∴∠A=∠CBE,
∴AD∥BC(同位角相等,两直线平行);
(3)BC平分∠DBE.
理由如下:
∵AD平分∠BDF,
∴∠FDA=∠ADB,
∵AE∥CF,AD∥BC,
∴∠FDA=∠A=∠CBE,∠ADB=∠CBD,
∴∠EBC=∠CBD,
∴BC平分∠DBE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一家商店准备进行装修,若请甲、乙两个装修队同时施工,8天完成,需付两队共3520元费用;若先请甲队单独做6天,再请乙队单独做12天可以完成,需付两队共3480元费用。
(1)甲、乙两队工作一天,商场各应付多少元?
(2)单独请哪个队装修,商场所付费用最少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了测量出楼房AC的高度,从距离楼底C处60
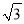 米的点D(点D与楼底C在同一水平上)出发,沿斜面坡度为i=l:
米的点D(点D与楼底C在同一水平上)出发,沿斜面坡度为i=l: 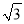 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53
的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53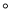 ,求楼房AC的高度(参考数据:sin53
,求楼房AC的高度(参考数据:sin53 =
=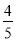 , cos53
, cos53 =
=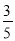 , tan53
, tan53 =
=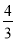 ,
, 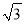 ≈1.732,结果精确到0.1米)
≈1.732,结果精确到0.1米)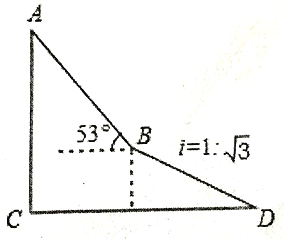
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知AB是⊙0的直径,AP是⊙0的切线,A是切点,BP与⊙0交于点C.
(1)如图①,若AB=2,∠P=30
 ,求AP的长.(结果保留根号)
,求AP的长.(结果保留根号)(2)如图②,若D为AP的中点,∠P=30
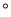 ,求证:直线CD是⊙O的切线.
,求证:直线CD是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】盐城市大力发展绿色交通,构建公共绿色交通体系,“共享单车”的投入使用给人们的出行带来便利,小明随机调查了若干市民租用共享单车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如图所示的统计图,请根据图中信息,解答下列问题:

(1)这次被调査的总人数是 ;
(2)补全条形统计图;
(3)在扇形统计图中,求表示A组(t≤10分)的扇形圆心角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某气球内充满一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.

(1)写出这一函数的表达式.
(2)当气体体积为1 m3时,气压是多少?
(3)当气球内的气压大于140 kPa时,气球将爆炸,为了安全考虑,气体的体积应不小于多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知抛物线
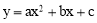 经过点A(0,3),B(3,0),C(4,3).
经过点A(0,3),B(3,0),C(4,3).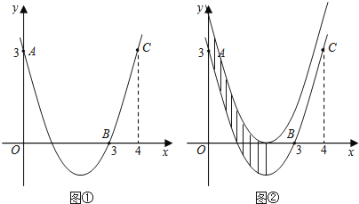
(1)求抛物线的函数表达式;
(2)求抛物线的顶点坐标和对称轴;
(3)把抛物线向上平移,使得顶点落在x轴上,直接写出两条抛物线、对称轴和y轴围成的图形的面积S(图②中阴影部分).
相关试题

