【题目】如图，在直角坐标系中，O为原点．点A在x轴的正半轴上，点B在y轴的正半轴上，tan∠OAB=2．二次函数y=x2+mx+2的图象经过点A，B，顶点为D．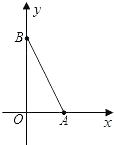

（1）求这个二次函数的解析式；
（2）将△OAB绕点A顺时针旋转90°后，点B落到点C的位置．将上述二次函数图象沿y轴向上或向下平移后经过点C．请直接写出点C的坐标和平移后所得图象的函数解析式；
（3）设（2）中平移后所得二次函数图象与y轴的交点为B1 ， 顶点为D1 ． 点P在平移后的二次函数图象上，且满足△PBB1的面积是△PDD1面积的2倍，求点P的坐标．

参考答案：

【答案】
（1）解：由题意，点B的坐标为（0，2），

∴OB=2，

∵tan∠OAB=2，即 =2．

∴OA=1．

∴点A的坐标为（1，0）．

又∵二次函数y=x2+mx+2的图象过点A，

∴0=12+m+2．

解得m=﹣3，

∴所求二次函数的解析式为y=x2﹣3x+2


（2）解：作CE⊥x轴于E，

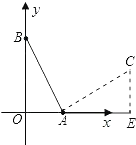
由于∠BAC=90°，可知∠CAE=∠OBA，△CAE≌△OBA，

可得CE=OA=1，AE=OB=2，可得点C的坐标为（3，1）．

由于沿y轴运动，故图象开口大小、对称轴均不变，

设出解析式为y=x2﹣3x+c，代入C点作标得1=9﹣9+c，c=1，

所求二次函数解析式为y=x2﹣3x+1．


（3）解：由（2），经过平移后所得图象是原二次函数图象向下平移1个单位后所得的图象，

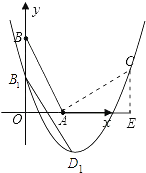
那么对称轴直线x= 不变，且BB1=DD1=1．

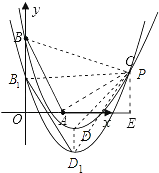
∵点P在平移后所得二次函数图象上，

设点P的坐标为（x，x2﹣3x+1）．

在△PBB1和△PDD1中，∵S△PBB1=2S△PDD1，

∴边BB1上的高是边DD1上的高的2倍．

①当点P在对称轴的右侧时，x=2（x﹣ ），得x=3，

∴点P的坐标为（3，1）；

②当点P在对称轴的左侧，同时在y轴的右侧时，x=2（ ﹣x），得x=1，

∴点P的坐标为（1，﹣1）；

③当点P在y轴的左侧时，x＜0，又﹣x=2（ ﹣x），

得x=3＞0（舍去），

∴所求点P的坐标为（3，1）或（1，﹣1）


【解析】（1）二次函数y=x2+mx+2的图象经过点B，可得B点坐标为（0，2），再根据tan∠OAB=2求出A点坐标，将A代入解析式即可求得函数解析式；（2）根据旋转不变性可轻松求得C点坐标，由于沿y轴运动，故图象开口大小、对称轴均不变，设出解析式，代入C点作标即可求解；（3）由于P点位置不固定，由图可知要分①当点P在对称轴的右侧时，②当点P在对称轴的左侧，同时在y轴的右侧时，③当点P在y轴的左侧时，三种情况讨论．

关闭