【题目】如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD. 
(1)求证:BD平分∠ABH;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
参考答案:
【答案】
(1)证明:连接OD,
∵EF是⊙O的切线,
∴OD⊥EF,
又∵BH⊥EF,
∴OD∥BH,
∴∠ODB=∠DBH,
∵OD=OB,
∴∠ODB=∠OBD
∴∠OBD=∠DBH,
即BD平分∠ABH.
(2)解:过点O作OG⊥BC于点G,则BG=CG=4,
在Rt△OBG中,OG= ![]() =
= ![]() =
= ![]() .
.
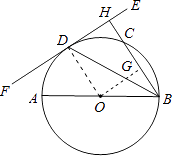
【解析】(1)连接OD,根据切线的性质以及BH⊥EF,即可证得OD∥BC,然后根据等边对等角即可证得;(2)过点O作OG⊥BC于点G,则利用垂径定理即可求得BG的长,然后在直角△OBG中利用勾股定理即可求解.
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握垂径定理(垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小敏和小强到某厂参加社会实践活动,该厂用白板纸做包装盒,每张白板纸可裁成3个盒身或5个盒盖,且一个盒身和两个盒盖恰好能做成一个包装盒.设裁成盒身的白板纸有x张,请回答下列问题:
(1)若有11张白板纸.
①请完成下表:
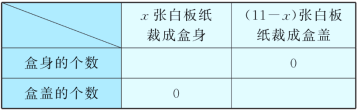
②问:最多可做多少个包装盒.
(2)若仓库中已有4个盒身,3个盒盖和23张白板纸,现把白板纸分成两部分,一部分裁成盒身,一部分裁成盒盖.当盒身与盒盖全部配套用完时,可做多少个包装盒?
(3)若有n张白板纸(70≤n≤80),先把一张白板纸裁出2个盒身和1个盒盖(余下一点边角料不要),剩下白板纸分成两部分,一部分裁成盒身,一部分裁成盒盖.当盒身与盒盖全部配套用完时,n的值可以是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是边长为2的正方形,点G是BC延长线上一点,连接AG,点E、F分别在AG上,连接BE、DF,∠1=∠2,∠3=∠4.
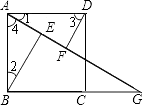
(1)证明:△ABE≌△DAF;
(2)若∠AGB=30°,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB交CD于O,OE⊥AB.
(1)若∠EOD=20°,求∠AOC的度数;
(2)若∠AOC:∠BOC=1:2,求∠EOD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.

(1)当a=﹣ 时,①求h的值;②通过计算判断此球能否过网.
时,①求h的值;②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为 m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,O为原点.点A在x轴的正半轴上,点B在y轴的正半轴上,tan∠OAB=2.二次函数y=x2+mx+2的图象经过点A,B,顶点为D.
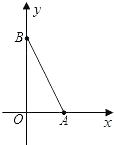
(1)求这个二次函数的解析式;
(2)将△OAB绕点A顺时针旋转90°后,点B落到点C的位置.将上述二次函数图象沿y轴向上或向下平移后经过点C.请直接写出点C的坐标和平移后所得图象的函数解析式;
(3)设(2)中平移后所得二次函数图象与y轴的交点为B1 , 顶点为D1 . 点P在平移后的二次函数图象上,且满足△PBB1的面积是△PDD1面积的2倍,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程(组)解应用题
《九章算术》是中国古代第一部数学专著,也是世界上最早的印刷本数学书它的出现标志着中国古代数学体系的形成.《九章算术》早在隋唐时期即已传入朝鲜、日本并被译成日、俄、德、法等多种文字版本.书中有如下问题:今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?
大意是:有几个人一起去买一件物品,如果每人出8元,则多了3元;如果每人出7元,则少了4元钱,问有多少人?该物品价值多少元?
相关试题

