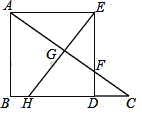
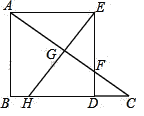
【题目】如图,在Rt△ABC中,∠B=90°,BC>AB,在BC边上取点D,使AB=BD,构造正方形ABDE,DE交AC于点F,作EG⊥AC交AC于点G,交BC于点H.
(1)求证:△AEF≌△EDH.
(2)若AB=3,DH=2DF,求BC的长.
参考答案:
【答案】(1)证明见解析;(2)4.5
【解析】
(1)根据正方形的性质,通过“角边角”即可得证;
(2)设DF=x,则DH=2x,由(1)可得ED=EF+DF=3x=AB,易证△DFC∽△BAC,则![]() ,求得DC=
,求得DC=![]() ,进而求得BC的长.
,进而求得BC的长.
证明:(1)∵四边形ABDE是正方形,
∴AE=DE,∠AED=∠EDH=90°,
∵EG⊥AC,
∴∠AGE=90°,
∴∠GAE+∠AEG=∠AEG+∠DEH=90°,
∴∠GAE=∠DEH,
在△AEF和△EDH中,
∵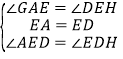 ,
,
∴△AEF≌△EDH(ASA);
(2)设DF=x,则DH=2x,
∵△AEF≌△EDH.
∴EF=DH=2x,
∴ED=EF+DF=3x=AB,
∵四边形ABDE是正方形,
∴AB∥DF,
∴△DFC∽△BAC,
∴![]() ,
,
∵BD=3,
∴DC=![]() ,
,
∴BC=BD+CD=3+![]() =4.5.
=4.5.
-
科目: 来源: 题型:
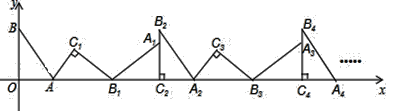
查看答案和解析>>【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B,O分别落在点B1,C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(3,0),B(0,4),则点B2018的坐标为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为坐标原点,B在x轴上,四边形OACB为平行四边形,且
∠AOB=60°,反比例函数
 (k>0)在第一象限内过点A,且与BC交于点F。当F为BC的中点,且S△AOF=12
(k>0)在第一象限内过点A,且与BC交于点F。当F为BC的中点,且S△AOF=12 时,OA的长为____.
时,OA的长为____.
-
科目: 来源: 题型:
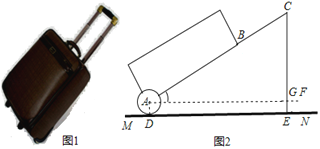
查看答案和解析>>【题目】有一只拉杆式旅行箱如图1,其侧面示意图如图2所示,已知箱体长AB=50 cm,拉杆BC的伸长距离最大时可达35 cm,点A、B、C在同一条直线上,在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面切于点D,在拉杆伸长至最大的情况下,当点B到水平地面MN的距离为38 cm时,点C到水平面的距离CE为59 cm.设AF∥MN,AF交CE于点G(精确到1 cm,参考数据:sin64°≈0.90,cos64°≈0.39,tan64°≈2.1)
(1)求⊙A的半径长;
(2)当人的手自然下垂拉旅行箱时,人感觉较为舒服,某人将手自然下垂在C端拉旅行箱时,CE为80 cm,∠CAF=64°.求此时拉杆BC的伸长距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市智慧阅读活动正如火如茶地进行.某班学习委员为了解11月份全班同学课外阅读的情况,调查了全班同学11月份读书的册数,并根据调查结果绘制了如下不完整的条形统计图和扇形统计图:
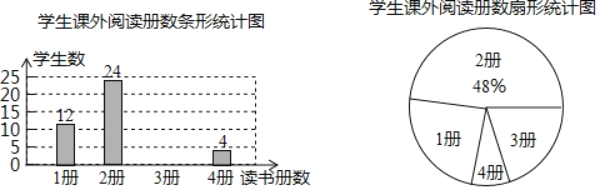
(1)扇形统计图中“3册”部分所对应的圆心角的度数是 ,并把条形统计图补充完整;
(2)该班的学习委员11月份的读书册数为4册,若该班的班主任从11月份读书4册的学生中随机抽取两名同学参加学校举行的知识竞赛,请用列表法或画树状图求恰好有一名同学是学习委员的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“一带一路”的战略构想为国内许多企业的发展带来了新的机遇,某公司生产A,B两种机械设备,每台B种设备的成本是A种设备的1.5倍,公司若投入16万元生产A种设备,36万元生产B种设备,则可生产两种设备共10台.请解答下列问题:
(1)A、B两种设备每台的成本分别是多少万元?
(2)若A,B两种设备每台的售价分别是6万元,10万元,公司决定生产两种设备共60台,计划销售后获利不低于126万元,且A种设备至少生产53台,求该公司有几种生产方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,等边△ABC内接于⊙O,点P是⌒AB上的任意一点,连结PA,PB,PC.点D是PC上一点,连结DB.
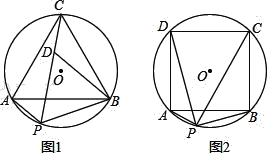
(1) 若PD=PB,求∠PBD的度数;
(2)在(1)的条件下,小丽探究
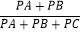 的值,她认为只要弄清PA+PB与PC的关系即可,她的思路可以用以下框图表示:
的值,她认为只要弄清PA+PB与PC的关系即可,她的思路可以用以下框图表示:
根据小丽的思路,请你完整地书写本题的探究过程,并求出
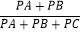 的值.
的值.(3)如图2,把条件“等边△ABC”改为“正方形ABCD”,其余条件不变,判断
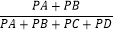 是定值吗?若是,请求出这个值;若不是,请说明理由.
是定值吗?若是,请求出这个值;若不是,请说明理由.
相关试题

