【题目】如图,AE是△ABC的角平分线,AD⊥BC于点D,点F为BC的中点,若∠BAC=104°,∠C=40°,则有下列结论:①∠BAE=52°;②∠DAE=2°;③EF=ED;④S△ABF=![]() S△ABC.其中正确的个数有( )
S△ABC.其中正确的个数有( )
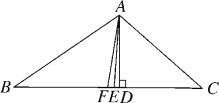
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】C
【解析】
根据角平分线的定义可判定①;根据角平分线的定义及垂直的定义求得∠CAE=52°,∠CAD=50°,再由∠DAE=∠CAE -∠CAD即可判定②;根据三角形中线的性质即可判定④;③根据已知条件判定不出,由此即可解答.
∵AE是△ABC的角平分线,∠BAC=104°,
∴∠BAE=∠CAE=![]() =52°;
=52°;
①正确;
∵AD⊥BC,∠C=40°,
∴∠CAD=90°-40°=50°;
∴∠DAE=∠CAE -∠CAD =2°;
②正确;
∵F为BC的中点,
∴S△ABF=![]() S△ABC.
S△ABC.
④正确.
根据已知条件不能够判定③正确.
综上,正确的结论为①②④,共3个,故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有下列四种结论:①AB=AD;②∠B=∠D;③∠BAC=∠DAC;④BC=DC.以其中的2个结论作为依据不能判定△ABC≌△ADC的是( )
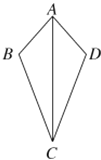
A. ①② B. ①③ C. ①④ D. ②③
-
科目: 来源: 题型:
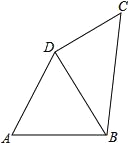
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=AD=8,∠A=60°,∠ADC=150°,四边形ABCD的周长为32.
(1)求∠BDC的度数;
(2)四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
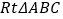 中,
中,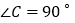 ,把
,把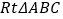 绕着
绕着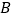 点逆时针旋转,得到
点逆时针旋转,得到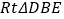 ,点
,点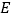 在
在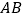 上.
上.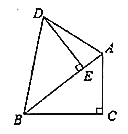
(1)若
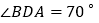 ,求得
,求得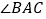 度数;
度数;(2)若
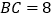 ,
,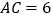 ,求
,求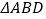 中
中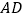 边上的高.
边上的高. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是工人师傅用同一种材料制成的金属框架,已知∠B=∠E,AB=DE,BF=EC,其中△ABC的周长为24cm,CF=3cm,则制成整个金属框架所需这种材料的总长度为 ________cm.

-
科目: 来源: 题型:
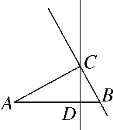
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=7cm,BC=3cm,CD为AB边上的高.点E从点B出发在直线BC上以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F.当点E运动________s时,CF=AB.
-
科目: 来源: 题型:
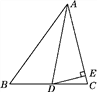
查看答案和解析>>【题目】在△ABC中,AD是角平分线,∠B=54°,∠C=76°.
(1)求∠ADB和∠ADC的度数;
(2)若DE⊥AC,求∠EDC的度数.
相关试题

