【题目】如图,有下列四种结论:①AB=AD;②∠B=∠D;③∠BAC=∠DAC;④BC=DC.以其中的2个结论作为依据不能判定△ABC≌△ADC的是( )
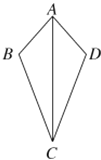
A. ①② B. ①③ C. ①④ D. ②③
参考答案:
【答案】A
【解析】
根据全等三角形的判定方法:SSS、SAS、ASA、AAS、HL依次对各选项分析判断即可.
A、由AB=AD,∠B=∠D,虽然AC=AC,但是SSA不能判定△ABC≌△ADC,故A选项与题意相符;
B、由①AB=AD,③∠BAC=∠DAC,又AC=AC,根据SAS,能判定△ABC≌△ADC,故B选项与题意不符;
C、由①AB=AD,④BC=DC,又AC=AC,根据SSS,能判定△ABC≌△ADC,故C选项与题意不符;
D、由②∠B=∠D,③∠BAC=∠DAC,又AC=AC,根据AAS,能判定△ABC≌△ADC,故D选项与题意不符;
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连接EC.
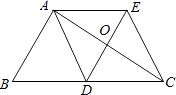
(1)求证:AD=EC;
(2)当∠BAC=90°时,求证:四边形ADCE是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC是一张等腰直角三角形纸板,∠C=90°,AC=BC=2,
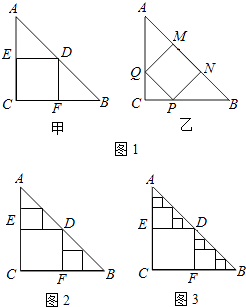
(1)要在这张纸板中剪出一个尽可能大的正方形,有甲、乙两种剪法(如图1),比较甲、乙两种剪法,哪种剪法所得的正方形面积大?请说明理由.
(2)图1中甲种剪法称为第1次剪取,记所得正方形面积为s1;按照甲种剪法,在余下的△ADE和△BDF中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为s2(如图2),则s2=;再在余下的四个三角形中,用同样方法分别剪取正方形,得到四个相同的正方形,称为第3次剪取,并记这四个正方形面积和为s3 , 继续操作下去…,则第10次剪取时,s10=;
(3)求第10次剪取后,余下的所有小三角形的面积之和. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两直线l1 , l2分别经过点A(1,0),点B(﹣3,0),并且当两直线同时相交于y正半轴的点C时,恰好有l1⊥l2 , 经过点A、B、C的抛物线的对称轴与直线l1交于点K,如图所示.
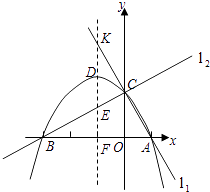
(1)求点C的坐标,并求出抛物线的函数解析式;
(2)抛物线的对称轴被直线l1 , 抛物线,直线l2和x轴依次截得三条线段,问这三条线段有何数量关系?请说明理由;
(3)当直线l2绕点C旋转时,与抛物线的另一个交点为M,请找出使△MCK为等腰三角形的点M,简述理由,并写出点M的坐标. -
科目: 来源: 题型:
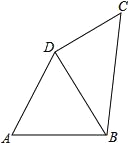
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=AD=8,∠A=60°,∠ADC=150°,四边形ABCD的周长为32.
(1)求∠BDC的度数;
(2)四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
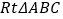 中,
中,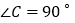 ,把
,把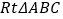 绕着
绕着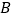 点逆时针旋转,得到
点逆时针旋转,得到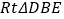 ,点
,点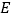 在
在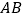 上.
上.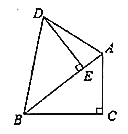
(1)若
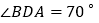 ,求得
,求得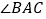 度数;
度数;(2)若
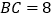 ,
,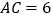 ,求
,求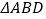 中
中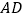 边上的高.
边上的高. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AE是△ABC的角平分线,AD⊥BC于点D,点F为BC的中点,若∠BAC=104°,∠C=40°,则有下列结论:①∠BAE=52°;②∠DAE=2°;③EF=ED;④S△ABF=
 S△ABC.其中正确的个数有( )
S△ABC.其中正确的个数有( )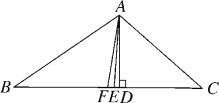
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

