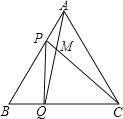
【题目】点P、Q分别是边长为4cm的等边![]() 的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都是
的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都是![]() ,设运动时间为t秒.
,设运动时间为t秒.
![]() 连接AQ、CP交于点M,则在P、Q运动的过程中,
连接AQ、CP交于点M,则在P、Q运动的过程中,![]() 变化吗:若变化,则说明理由,若不变,则求出它的度数;
变化吗:若变化,则说明理由,若不变,则求出它的度数;
![]() 连接PQ,
连接PQ,
![]() 当
当![]() 秒时,判断
秒时,判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 当
当![]() 时,则
时,则![]() ______秒
______秒![]() 直接写出结果
直接写出结果![]()
参考答案:
【答案】(1)在P、Q运动的过程中,∠CMQ不变,∠CMQ=60°;(2)①△BPQ是等边三角形;②![]() .
.
【解析】
(1)先证明△ABQ≌△CAP,得到∠BAQ=∠ACP,根据∠BAQ+∠QAC=60°,然后利用三角形外角的性质即可得出结论;
(2)①当t=2秒时,AP=BQ=2,PB=4﹣2=2,可知△BPQ是等边三角形;
②当PQ⊥BC时,∠B=60°,根据直角三角形30°所对直角边等于斜边一半的性质列等量关系,即可求出时间t.
(1)∵△ABC为等边三角形,
∴AB=AC,∠B=∠PAC=60°,
∵点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,
∴AP=BQ,
在△APC和△BQA中
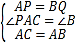 ,
,
∴△APC≌△BQA(SAS),
∴∠BAQ=∠ACP,
∴∠CMQ=∠CAQ+∠ACP=∠BAQ+∠CAQ=∠BAC=60°,
∴在P、Q运动的过程中,∠CMQ不变,∠CMQ=60°;
故答案为:在P、Q运动的过程中,∠CMQ不变,∠CMQ=60°.
(2)①∵运动时间为ts,则AP=BQ=t,
∴PB=4﹣t,
当t=2秒时,AP=BQ=2,PB=4﹣2=2,∴AP=BQ=PB,
∴△BPQ是等边三角形;
故答案为:△BPQ是等边三角形.
②∵运动时间为ts,则AP=BQ=t,∴PB=4﹣t,
∵PQ⊥BC,∴∠PQB=90°,
∵∠B=60°,∴PB=2BQ,
∴4﹣t=2t,解得t=![]() ,
,
故答案为:t=![]() .
.
-
科目: 来源: 题型:
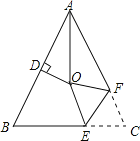
查看答案和解析>>【题目】如图,在
 中,
中, ,
,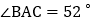 ,
,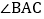 的平分线与AB的垂直平分线交于点O,将
的平分线与AB的垂直平分线交于点O,将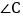 沿EF折叠,若点C与点O恰好重合,则
沿EF折叠,若点C与点O恰好重合,则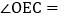 ______.
______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组
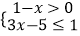 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
A.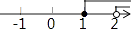
B.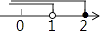
C.
D.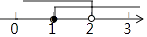
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于反比例函数y=
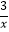 ,下列说法中正确的是( )
,下列说法中正确的是( )
A.它的图象分布在第二、四象限
B.它的图象过点(﹣6,﹣2)
C.当x<0时,y的值随x的增大而减小
D.与y轴的交点是(0,3) -
科目: 来源: 题型:
查看答案和解析>>【题目】某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活的情况进行调查统计,并绘制了如图所示的统计图,根据统计图提供的信息解决下列问题:

(1)这种树苗成活的频率稳定在___________,成活的概率估计值为___________.
(2)该地区已经移植这种树苗5万棵.
①估计这种树苗成活___________万棵.
②如果该地区计划成活18万棵这种树苗,那么还需移植这种树苗约多少万棵?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“双十二”期间,A,B两个超市开展促销活动,活动方式如下:
A超市:购物金额打9折后,若超过2000元再优惠300元;
B超市:购物金额打8折.
某学校计划购买某品牌的篮球做奖品,该品牌的篮球在A,B两个超市的标价相同.根据商场的活动方式:
(1)若一次性付款4200元购买这种篮球,则在B商场购买的数量比在A商场购买的数量多5个.请求出这种篮球的标价;
(2)学校计划购买100个篮球,请你设计一个购买方案,使所需的费用最少.(直接写出方案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直线AB分别交x轴、y轴于点
 点
点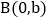 且a、b满足
且a、b满足 .
.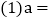 ______;
______;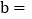 ______.
______. 点P在直线AB的右侧,且
点P在直线AB的右侧,且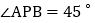 ,
, 若点P在x轴上,则点P的坐标为______;
若点P在x轴上,则点P的坐标为______; 若
若 为直角三角形,求点P的坐标;
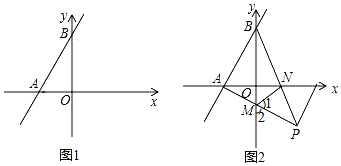
为直角三角形,求点P的坐标; 如图2,在
如图2,在 的条件下,
的条件下,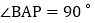 且点P在第四象限,AP与y轴交于点M,BP与x轴交于点N,连接
且点P在第四象限,AP与y轴交于点M,BP与x轴交于点N,连接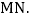 求证:
求证: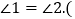 提示:过点P作
提示:过点P作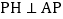 交x轴于
交x轴于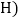
相关试题

