搜索
【题目】已知扇形的半径为6cm，圆心角为150°，则此扇形的弧长是cm，扇形的面积是cm2（结果保留π）．
参考答案：
【答案】5π；15π
【解析】解：∵扇形的半径为6cm，圆心角为150°， ∴此扇形的弧长是：l= 
=5π（cm），
根据扇形的面积公式，得
S扇= 
=15π（cm2）．
所以答案是：5π，15π．
【考点精析】根据题目的已知条件，利用弧长计算公式和扇形面积计算公式的相关知识可以得到问题的答案，需要掌握若设⊙O半径为R，n°的圆心角所对的弧长为l，则l=nπr/180;注意：在应用弧长公式进行计算时，要注意公式中n的意义．n表示1°圆心角的倍数，它是不带单位的；在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两地之间有一条笔直的公路L，小明从甲地出发沿公路L步行前往乙地，同时小亮从乙地出发沿公路L骑自行车前往甲地，小亮到达甲地停留一段时间，原路原速返回，追上小明后两人一起步行到乙地．设小明与甲地的距离为y1米，小亮与甲地的距离为y2米，小明与小亮之间的距离为s米，小明行走的时间为x分钟．y1、y2与x之间的函数图象如图1，s与x之间的函数图象（部分）如图2．
（1）求小亮从乙地到甲地过程中y2（米）与x（分钟）之间的函数关系式；
（2）求小亮从甲地返回到与小明相遇的过程中s（米）与x（分钟）之间的函数关系式；
（3）在图2中，补全整个过程中s（米）与x（分钟）之间的函数图象，并确定a的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠C=90°，BC=3，AB=5．点P从点B出发，以每秒1个单位长度沿B→C→A→B的方向运动；点Q从点C出发，以每秒2个单位沿C→A→B方向的运动，到达点B后立即原速返回，若P、Q两点同时运动，相遇后同时停止，设运动时间为t秒．
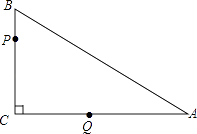
（1）当t=时，点P与点Q相遇；
（2）在点P从点B到点C的运动过程中，当t为何值时，△PCQ为等腰三角形？
（3）在点Q从点B返回点A的运动过程中，设△PCQ的面积为S平方单位．
①求S与t之间的函数关系式；
②当S最大时，过点P作直线交AB于点D，将△ABC中沿直线PD折叠，使点A落在直线PC上，求折叠后的△APD与△PCQ重叠部分的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数y=ax2+bx+c（a、b、c为常数且a≠0）中的x与y的部分对应值如下表：
x
﹣3
﹣2
﹣1
0
1
2
3
4
5
y
12
5
0
﹣3
﹣4
﹣3
0
5
12
给出了结论：
1）二次函数y=ax2+bx+c有最小值，最小值为﹣3；
2）当
时，y＜0；
3）二次函数y=ax2+bx+c的图象与x轴有两个交点，且它们分别在y轴两侧．则其中正确结论的个数是（ ）
A.3
B.2
C.1
D.0 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC内接于⊙O，∠BAC=120°，AB=AC，BD为⊙O的直径，AD=6，则DC= ．
-
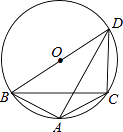
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，已知第一象限内的点A在反比例函数
的图象上，第二象限内的点B在反比例函数 
的图象上，连接OA、OB，若OA⊥OB，OB= 
OA，则k= ． -
科目： 来源： 题型：
查看答案和解析>>【题目】解方程组和分式方程：
（1）
（2）
．
相关试题
